BANDGAP

BANDGAP = COMPACT | WEIGHT | KPOINT
Default: BANDGAP = COMPACT

Description: BANDGAP determines the verbosity for reporting the bandgap to the OUTCAR file.

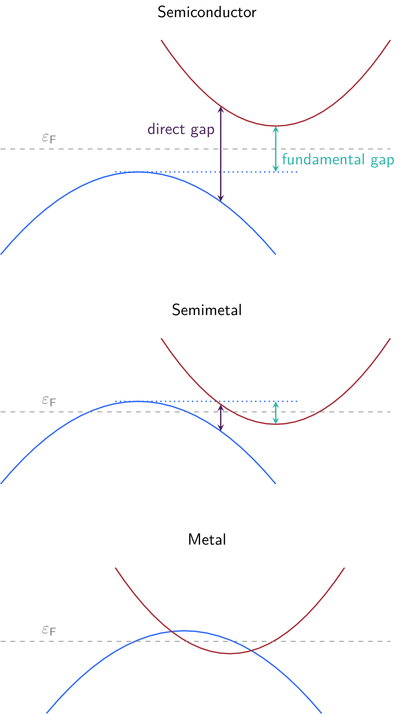
For semiconductor, the bandgap the direct and fundamental bandgap have a clear definition. For semimetals, the Fermi energy cuts through bands so the depending on the method one defines either a zero or a negative fundamental bandgap. For metals, defining a bandgap is not meaningful.

The bandgap of the system separates the occupied valence bands from the unoccupied conduction bands. Of particular interest are the fundamental bandgap between valence band maximum (VBM) and conduction band minimum (CBM) and the direct bandgap at a single k point.

BANDGAP controls how VASP reports the bandgap information. The following options exist:

BANDGAP=COMPACT

Uses Fermi weights to decide what valence and conduction bands are. Reports the VBM, CBM, and fundamental gap to the OUTCAR file.

BANDGAP=WEIGHT

Uses Fermi weights to decide what valence and conduction bands are. Provides a comprehensive report of all band extrema.

BANDGAP=KPOINT

Considers each k point individually to decide what valence and conduction bands are. Provides a comprehensive report of all band extrema.

The figure illustrates different possible properties of electronic band structures. For semiconductors, the bandgap is well defined so that the choice of BANDGAP only effects whether the output is compact or verbose. For metals, there is no straightforward definition of a bandgap so that the default of BANDGAP=COMPACT is sufficient. A semimetal shares properties with metals (Fermi energy crosses bands) and with semiconductors (visible bandgap in the band structure).

BANDGAP=WEIGHT interprets systems like a metal; valence (conduction) states are more (less) than half filled. In this case, the bandgap of a semimetal converges to zero with increasing number of k points similar to a metal. For N number of electrons, the number of valence states is not in general equal to N for all k points. Hence, the direct bandgap is not necessarily between the N-th and the (N + 1)-th state.

BANDGAP=KPOINT considers systems like a semiconductor where every k point may be treated individually. The number of valence bands is equal to the number of electrons N for all k points and the direct bandgap is equal to the smallest difference between the N-th and (N + 1)-th state. In a semimetal, this approach produces a negative bandgap because the Fermi energy crosses the bands. For collinear calculations (ISPIN=2), this method will allow for a different number of up and down electrons at every k point.

Mind: Setting BANDGAP=KPOINT only impacts the output of VASP. It is not considered when evaluating the occupations of different bands. If you want to enforce certain occupations, please consider the tags NUPDOWN, FERWE, and FERDO.

Related tags and articles