BANDGAP
BANDGAP = COMPACT | WEIGHT | KPOINT
Default: BANDGAP = COMPACT
Description: BANDGAP determines the verbosity for reporting the bandgap to the OUTCAR file. Only the first character is significant.
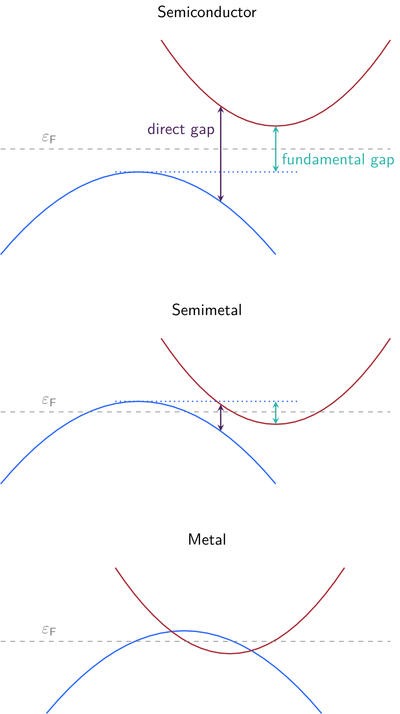
The bandgap of the system separates the occupied valence bands from the unoccupied conduction bands. Of particular interest are the fundamental bandgap between valence band maximum (VBM) and conduction band minimum (CBM) and the direct bandgap at a single k point.
BANDGAP controls how VASP reports the bandgap information. The following options exist:
- BANDGAP=COMPACT
- Uses Fermi weights to decide what valence and conduction bands are. Reports the VBM, CBM, and fundamental gap to the OUTCAR file.
- BANDGAP=WEIGHT
- Uses Fermi weights to decide what valence and conduction bands are. Provides a comprehensive report of all band extrema.
- BANDGAP=KPOINT
- Considers each k point individually to decide what valence and conduction bands are. Provides a comprehensive report of all band extrema.
Difference between WEIGHT and KPOINT
The figure illustrates different possible properties of electronic band structures. For semiconductors, the bandgap is well defined so that the choice of BANDGAP only affects whether the output is compact or verbose. For metals, there is no straightforward definition of a bandgap so the default of BANDGAP=COMPACT is sufficient. A semimetal shares properties with metals (Fermi energy crosses bands) and with semiconductors (visible bandgap in the band structure).
BANDGAP=WEIGHT interprets systems like a metal; valence (conduction) states are more (less) than half-filled. In this case, the bandgap of a semimetal converges to zero with an increasing number of k points similar to a metal. For N number of electrons, the number of valence states is not in general equal to N for all k points. Hence, the direct bandgap is not necessarily between the N-th and the (N + 1)-th state.
BANDGAP=KPOINT considers systems like a semiconductor where every k point may be treated individually. The number of valence bands is equal to the number of electrons N for all k points and the direct bandgap is equal to the smallest difference between the N-th and (N + 1)-th state. In a semimetal, this approach produces a negative bandgap because the Fermi energy crosses the bands. For collinear calculations (ISPIN=2), this method will allow for a different number of up and down electrons at every k point.
| Mind: Setting BANDGAP=KPOINT only impacts the output of VASP. It is not considered when evaluating the occupations of different bands. If you want to enforce certain occupations, please consider the tags NUPDOWN, FERWE, and FERDO. |
Example of the verbose output
Band structure
--------------
spin independent spin component 1 spin component 2
val. band max: 9.679953 9.679953 5.987917
cond. band min: 9.148387 10.409707 9.148387
fundamental gap: -0.531566 0.729754 3.160470
VBM @ kpoint: 0.2949 0.4423 0.1474 0.2949 0.4423 0.1474 0.0000 -0.0000 0.0000
CBM @ kpoint: 0.5000 0.5000 0.0000 0.0000 0.0000 0.0000 0.5000 0.5000 0.0000
lower band: 8.126216 7.283444 5.087674
upper band: 9.386102 10.916258 9.148387
direct gap: 1.259885 3.632813 4.060713
@ kpoint: 0.3846 0.3846 0.0000 0.0641 0.0962 0.0321 0.5000 0.5000 0.0000
The column spin independent is always present and reports the bandgap ignoring the spin of the electron. The other two columns are only visible for ISPIN=2 and describe the bandgap for a given spin of the electron. The first block of rows show the band edges of the fundamental bandgap and their corresponding k-point coordinates. The second block reports analogous values for the direct gap. In each case the energy difference of the band edges is computed and printed as fundamental and direct gap, respectively.
