Best practices for machine-learned force fields

Using the machine-learning–force-fields method, VASP can construct force fields based on ab-initio simulations. There are many aspects to carefully consider while constructing, testing, retraining, and applying a force field. Here, we list some best practices but bear in mind that the list is incomplete and the method has not been applied to a large number of systems. Therefore, we recommend using the usual rigorous checking that is necessary for any research project. The basic steps needed to train a machine-learning force field can be found on the Basics page for machine-learning force fields.

Best practice training from scratch

To start a training run the user hast to set ML_MODE=TRAIN. If there is no ML_AB file present in the folder where vasp is executed the training algorithm will start from scratch. This implies that vasp has to do ab-initio calculations and therefore the first step is to set up the electronic minimization scheme.

Ab-initio calculation setup

In general anything which applies for VASP DFT calculations will also apply here. Users can use the guidelines for electronic-minimization to set up the ab-initio part for the on the fly training. Additionally, we strongly advise to follow this guidelines for the ab-initio calculation while on-the-fly learning:

• Do not set MAXMIX>0 when using machine learning force fields. During machine learning, the first principles calculations are often bypassed for hundreds or even thousands of ionic steps, and the ions might move considerably between first-principles calculations. In these cases using MAXMIX will very often lead to electronic divergence or strange errors during the self-consistency cycle.
• It is generally possible to train force fields on a smaller unit cell and then apply it to a larger system. Be careful to choose the structure large enough, so that the phonons or collective vibrations "fit" into the supercell.
• It is important to learn the correct forces. This requires converged electronic calculations concerning electronic parameters, i.e., the number of k-points, the plane-wave cutoff (ENCUT), electronic minimization algorithm, etc.
• Switch off the symmetry as in molecular-dynamics runs (ISYM=0).
• For simulations without fixed lattice, the plane-wave cutoff ENCUT needs to be set at least 30 percent higher than for fixed volume calculations. Also, it is good to restart often (ML_ISTART=1) to reinitialize the PAW basis of the KS orbitals and avoid Pulay stress.

Molecular dynamics Set-up

After obtaining forces by the Hellman-Feynman theorem from the electronic minimization VASP has to propagate the ions to obtain a new configuration in phase space. For the molecular dynamics part the user should be familiar with setting up Molecular dynamics runs. Additionally we recommend the following settings in the molecular dynamics part:

• Lower the integration step (POTIM) if the system contains light elements or increase the mass of the light elements (POMASS) in the INCAR or POTCAR file.
• If possible, heat the system gradually, making use of temperature ramping (set TEEND higher than TEBEG). Start from a low (nonzero) temperature and increase to a temperature approximately 30% higher than the desired application temperature. This helps to avoid an undesired state of the on-the-fly learning algorithm where only very few structures at the beginning of the MD run are sampled.
• If possible, prefer molecular-dynamics training runs in the NpT ensemble (ISIF=3). The additional cell fluctuations improve the robustness of the resulting force field. However, for liquids only volume changes of the supercell are allowed because otherwise the cell may "collapse", i.e., it will tilt extremely such that the system becomes a layer of atoms. This can be achieved with the ICONST file, see 3) and 4) here. The NVT ensemble (ISIF=2) is also acceptable for training, but use the Langevin thermostat, since it is very good for phase space sampling (ergodicity) due to its stochastic nature.
• One should always try to explore as much of the material's phase space as possible. Therefore, one should always avoid to train in the NVE ensemble.

General settings for on the fly training

The ML_MODE=TRAIN already sets widely applicable default values for the on the fly training during machine learning. Nevertheless, we would like to give the following guidelines to the user for setting individual machine learning parameters:

• When the system contains different components, train them separately first. For instance, when the system has a surface of a crystal and a molecule binding on that surface. First, train the bulk crystal, then the surface, next the isolated molecule, and finally the entire system. This way a significant amount of ab-initio calculation can be saved in the computationally most expensive combined system.
• If there are not enough reference configurations picked up during training (can be seen in ML_ABN) an adaption of the default value of ML_CTIFOR=0.02 to some lower value is advisable. The value of this tag strongly depends on the system under consideration and therefore the user is urged to determine a proper value of this flag by a trial and error procedure.
• A force field will always be only applicable for the phases of the material where it was trained in. So the machine-learned force fields are in general not expected to give reliable results for conditions where no training data is present.

Retraining

Besides on-the-fly training starting from scratch (ML_ISTART=0), VASP can also continue its learning from an existing database of structures or retrain from an already existing ML_AB file.

Continuation runs and retraining without re-selection of local reference configurations

In this mode of operation, that is ML_ISTART=1, a force field is first generated from the existing ML_AB file and then enhanced by continuing an MD run starting from the provided POSCAR file. While this mode was originally intended to improve or glue together existing force fields it can also be used to study the influence of different parameters when learning is based only on a fixed data set. For example, it is possible to investigate how the training errors depend on the descriptor cutoff radius. Or, whether a better fit quality can be achieved if the ridge regression is performed via singular-value decomposition (see further below). In order to retrain a given data set (ML_AB file) in the proposed way we can combine ML_ISTART=1 with NSW=0 and ML_CTIFOR=1000 in the INCAR file. NSW=0 will prevent the start of an additional on-the-fly MD run and hence stops VASP after learning the existing database. The large value for ML_CTIFOR ensures that no atom in the current POSCAR file qualifies as a learning candidate and prevents the execution of an ab-initio calculation for the POSCAR structure.

Retraining with re-selection of local reference configurations

This mode of operation is selected by ML_ISTART=3. In this mode a new machine learning force field is generated from ab-initio data provided in the ML_AB file. The structures are read in and processed one by one as if harvested via an MD simulation. In other words, the same steps are performed as in on-the-fly training but the source of data is not an MD run but the series of structures available in the ML_AB file. This operation mode can be used to generate VASP machine-learning force fields from pre-computed or external ab initio data sets. The important difference to ML_ISTART = 1 and NSW = 0 is that the list of local reference configurations in the ML_AB file is ignored and a new set if created. The new updated set is written to the final ML_ABN file. If calculations for ML_ISTART = 3 are too time consuming using the default settings, it is useful to increase ML_MCONF_NEW to values around 10-16 and set ML_CDOUB = 4. This often accelerates the calculations a factor 2-4. Furthermore, if the ML_AB file holds a wide variety of structures (for instance manually collected), we strongly recommend to avoid updates of ML_CTIFOR by setting ML_ICRITERIA = 0. In summary, the recommended settings are:

ML_ISTART = 3 ; ML_CTIFOR = 0.007 - 0.02 ; ML_ICRITERIA = 0; ML_MCONF_NEW = 16 ; ML_CDOUB = 4 ; NSW = 0

Vary ML_CTIFOR, and ML_CTIFOR only, until a satisfactory number of local reference configurations is found (i.e. until the fitting errors do not decrease as the number of local reference configuration increases). The number of local reference configurations increases as ML_CTIFOR becomes smaller. It is sometimes usefull to subsequently perform a more accurate SVD based regression.

Warning: This mode of operation is experimental and not yet heavily tested! Problems may arise, in particular if the ML_AB file contains structures with mixed number of elements and atom numbers.

Accuracy

The reachable accuracy of the force fields depends on many factors, e.g., species, temperature, pressure, electronic convergence, machine learning method, etc. In our implementation of the kernel-ridge regression, the accuracy of the force fields increases with an increasing number of local reference configurations. This increase is below linear and at the same time, the computational demand increases linearly. So the user has to trade-off between accuracy and efficiency.

Here are some empirical guidelines:

• For a given structure the error increases with increasing temperature and pressure. So the force field should not be trained in conditions that are too far away from the target condition. For example for a production run at 300K, it is good to learn above that temperature (450-500K) to be able to sample more structures that could appear in the production run, but it is not beneficial to learn the same phase at say 1000 K since this will likely lower the accuracy of the force-field.
• Liquids usually need many more training structures and local reference configurations to achieve similar accuracy as solids.
• Typical the fitting errors should be a few meV/atom for the energies and 30-100 meV/Angstrom for the forces at temperature between 300-1000 K. Errors that are slightly above these values can be potentially be acceptable, but those calculations should be thoroughly checked for correctness.

Accurate force fields

The default parameters controlling the learning and sampling are chosen to be a good compromise between accuracy and efficiency. Specifically, the default for ML_EPS_LOW tends to remove local reference configurations during the sparsification step, hence limiting the accuracy. However, further decreasing ML_EPS_LOW to below values of 1.0E-9 does not improve the accuracy, since the condition number of the regularized normal equation that is solved in the Bayesian regression is roughly proportional to the square of the condition number of the Gram matrix that is considered during sparsification (see here). So if the Gram matrix has a condition number of 1E9, then the normal equation has a condition number of 1E18, which implies that upon a solution of the normal equation loss of significance occurs.

To obtain highly accurate force fields that retain more local reference configurations, one needs to adopt the following two-step procedure:

First, perform a complete on the fly learning using:

ML_IALGO_LINREG=1; ML_SION1=0.3; ML_MRB1=12  

This can consist of many different training steps involving all desired structures. Increasing ML_MRB1 from 8 to 12 and decreasing ML_SION1 from 0.5 to 0.3 improves the condition number of the Gram matrix by about a factor 10, and allows the sparsification step to retain more local reference configurations (typically by about a factor 2). Of course, this will slow down the force field calculations somewhat.

If a complete retraining is not possible, you can also try to increase the number of local reference calculations only, as explained above, using ML_ISTART=3 and adding ML_SION1=0.3; ML_MRB1=12 to the recommended setting. Of course this will only lead to satisfactory results, if sufficient first principles data are available, but the number of local configuration is insufficient.

Second, refit the force-field using SVD:

NSW=0;  ML_IALGO_LINREG=3; ML_CTIFOR=1000.0; ML_EPS_LOW=1.0E-14;
ML_SION1=0.5; ML_MRB1= 8 

The second line is optional since it corresponds to the default values for the respective tags. The large value for ML_CTIFOR ensures that no additional ab initio calculation is performed. Since the condition number of the Gram matrix becomes worse when the width ML_SION1 is increased back to the default, ML_EPS_LOW must approach machine precision to avoid the sparsification step removing local reference configurations. Using SVD instead of solving the regularized normal equation avoids squaring the problem, and hence the condition number of the design matrix rather than its square matters. In our experience, an SVD refinement using a large ML_SION1=0.5 always improves the accuracy of the force field. That is, for a fixed database and a fixed set of local reference configurations, the larger ML_SION1 is the more accurate is the final MLFF.

Of course, the outlined procedure results in an MLFF with a slower execution time. Also, note that the improvements are typically only on the order of 10-20 %. Hence, whether it is worthwhile to pursue these steps depends on the desired application and accuracy. Also, the entire training needs to be redone from scratch, since the improvements can be only realized if more first principles data and more local reference configurations are supplied to the algorithm.

Monitoring

The monitoring of your learning can be divided into two parts:

• Molecular dynamics/ensemble-related quantities:
  • Monitor your structure visually. This means look at the CONTCAR or XDATCAR files with structure/trajectory viewers. Many times when something goes wrong it can be immediately traced back to unwanted or unphysical deformations.
  • Volume and lattice parameters in the OUTCAR and CONTCAR files. It is important to confirm that the average volume stays in the desired region. A strong change of the average volume over time in constant temperature and pressure runs indicates phase transitions or non-properly equilibrated systems.
  • Temperature and pressure in the OUTCAR and OSZICAR files. Strong deviations of temperature and pressure to the desired ones at the beginning of the calculation indicate non-properly equilibrated systems.
  • Use block averages to monitor the above characteristic values.
  • Pair-correlation functions (PCDAT).
• Machine learning specific quantities in the ML_LOGFILE file:
  • Estimation of required memory per core. It is written at the beginning of the ML_LOGFILE before allocations are done (see here). It is important that if the required memory exceeds the physically available memory the calculation won't necessarily immediately crash at the allocation of static arrays, since many systems use lazy allocations. The calculation could run for a long time before crashing with insufficient memory. Hence the memory estimation should always be checked after startup.
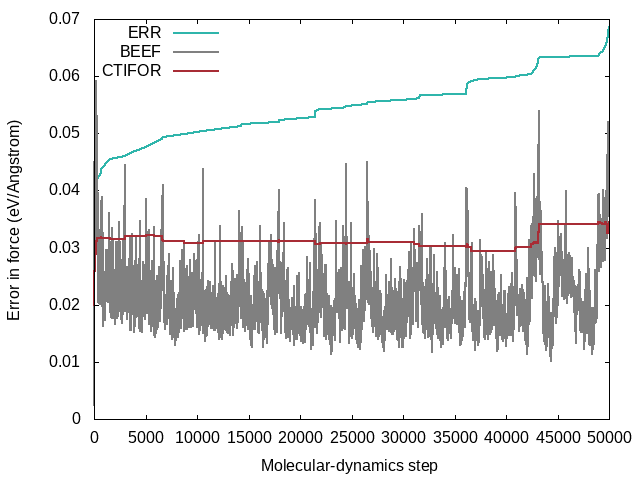
  • STATUS: Shows what happened at each molecular-dynamics steps. The force field is updated when the status is "learning/critical". Monitor this variable frequently from the beginning on (grep "STATUS" ML_LOGFILE.1|grep -E 'learning|critical'|grep -v "#"). If the calculation still updates the force field at every step after 50 iterations it is a sign that there is something seriously wrong with the calculation. The same is true if the calculation stops learning after a few steps and only force-field steps are carried out from then on. In both cases, no useful force field will come out. In ideal learning, the frequency of the update of the force field is high at the beginning and continuously decreases until the algorithm learns only sporadically. Note that due to the approximate error prediction of the Bayesian error the learning frequency will never drop to zero. If the learning frequency increases suddenly in the late stages of a molecular dynamics run, it is usually a sign that phase deformations happen that the current force field cannot describe well. These are most likely unwanted deformations that should be looked into carefully and are not be ignored.
  • LCONF: Number of local configurations at each learning step.
  • ERR: Root mean square error of predicted energy, forces, and stress ($O$) with respect to ab-initio data for all training structures up to the current molecular-dynamics step $\delta O=\sqrt{\sum\limits_{N}(O_{\mathrm{AI}}-O_{\mathrm{MLFF}})^{2}/N}$. Here $N$ goes over all training structures for the energies, element-wise over all training structures times number of atoms per structure times three Cartesian directions for the forces and element-wise over all training structures times nine tensor components for the stress tensor.
  • BEEF: Estimated Bayesian error of energy, forces and stress (columns 3-5). The current threshold for the maximum Bayesian error of forces ML_CTIFOR on column 6.
  • THRUPD: Update of ML_CTIFOR.
  • THRHIST: History of Bayesian errors used for ML_CTIFOR.

A typical evolution of the real errors (column 4 of ERR), Bayesian errors (column 4 of BEEF) and threshold (column 6 of BEEF) for the forces looks like the following:

The following commands were used to extract the errors from the ML_LOGFILE:

Click to show commands

grep ERR ML_LOGFILE|grep -v "#"|awk '{print $2, $4}' > ERR.dat

grep BEEF ML_LOGFILE|grep -v "#"|awk '{print $2, $4}' > BEEF.dat

grep BEEF ML_LOGFILE|grep -v "#"|awk '{print $2, $6}' > CTIFOR.dat

The following gnuplot script was used to plot the errors:

Click to show plot_errors.gnuplot

set key left top
set xlabel "Molecular-dynamics step"
set ylabel "Error in force (eV/Angstrom)"

set terminal png
set output 'ERR_BEEF_CTIFOR_vs_MD_step.png'

plot "ERR.dat" using 1:2 with lines lw 2 lt rgb "#2fb5ab" title "ERR", \
     "BEEF.dat" using 1:2 with lines lw 2 lt rgb "#808080" title "BEEF", \
     "CTIFOR.dat" using 1:2 with lines lw 2 lt rgb "#a82c35" title "CTIFOR"

• From the plot one can see that the Bayesian errors are always smaller than the real errors. Bayesian inference catches errors in the data well but still retains an error in the probability model.
• The plot was extracted from a heating run of liquid water. This can be nicely seen from the steadily increasing real error ERR over the whole calculation. In a constant temperature run the error would usually plateau after some time.
• The steps in the real error correspond to the molecular-dynamics steps where the force-field is updated ('learning' or 'critical' for the STATUS). This would be also evident from the change in the number of local reference configurations (grep "LCONF" ML_LOGFILE) at the same molecular-dynamics steps.
• The following things can cause an increase in the errors:
  • Using a temperature ramp always results in steadily increasing errors.
  • A sudden increase of the errors (especially after being stable for some time) usually indicates deformations of the cell. Usually one wants to avoid these deformations and only train the "collective vibrations" of a given phase at different temperatures. Common causes of these deformations are too large temperatures leading to phase transitions or neglect of constraints (ICONST file) for liquids.
  • The evidence approximation is over-fitting and the regularization cannot handle the over-fitting. This is a rare case, but if it happens one should start to reduce the fitting data by increasing ML_EPS_LOW.

Tuning on-the-fly parameters

In case too many or too few training structures and local reference configurations are selected some on-the-fly parameters can be tuned (for an overview of the learning and threshold algorithms we refer the user to here):

• ML_CTIFOR: Defines the learning threshold for the Bayesian error of the forces for each atom. In a continuation run, it can be set to the last value of ML_CTIFOR of the previous run. This way unnecessary sampling at the beginning of the calculation can be skipped. However, when going from one structure to the other, this tag should be very carefully set. ML_CTIFOR is species and system dependent. Low symmetry structures, for example, liquids, have usually a much higher error than high symmetry solids for the same compound. If a liquid is learned first and the last ML_CTIFOR from the liquid is used for the corresponding solid, this ML_CTIFOR is way too large for the solid and all predicted errors will be below the threshold. Hence no learning will be done on the solid. In this case, it is better to start with the default value for ML_CTIFOR.
• ML_CX: It is involved in the calculation of the threshold, ML_CTIFOR = (average of the stored Bayesian errors in the history) *(1.0 + ML_CX). This tag affects the frequency of selection of training structures and local reference configurations. Positive values of ML_CX result in a less frequent sampling (and hence less ab-initio calculations) and negative values result in the opposite. Typical values of ML_CX are between -0.3 and 0. For training runs using heating, the default usually results in very well-balanced machine-learned force fields. When the training is performed at a fixed temperature, it is often desirable to decrease to ML_CX=-0.1, to increase the number of first principle calculations and thus the size of the training set (the default can result in too few training data).
• ML_MHIS: Sets the number of previous Bayesian errors (from learning steps for the default of ML_ICRITERIA) that are used for the update of ML_CTIFOR. If, after the initial phase, strong variations of the Bayesian errors between updates of the threshold appear and the threshold also changes strongly after each update, the default of 10 for this tag can be lowered.
• ML_SCLC_CTIFOR: Scales ML_CTIFOR only in the selection of local reference configurations. In contrast, to ML_CX this tag does not affect the frequency of sampling (ab-initio calculations).
• ML_EPS_LOW: Controls the sparsification of the number of local reference configurations after they were selected by the Bayesian error estimation. Increasing ML_EPS_LOW increases the number of local reference configurations that are thrown away and by decreasing the opposite happens. This tag will also not affect the learning frequency since the sparsification is only done after the local reference configurations were selected for a new structure. We do not recommend increasing the threshold to values larger than 1E-7. Below that value this tag works nicely to control the number of local reference configurations, however, for multi-component systems, the sparsification algorithm tends to lead to strong imbalances in the number of local reference configurations for different species.
• ML_LBASIS_DISCARD: Controls, whether the calculation is continued or stopped after the maximum number of local reference configurations ML_MB for any species is reached. In the default behavior (ML_LBASIS_DISCARD=.FALSE.) the calculation stops and requests the user to increase ML_MB if the number of local reference configurations for any species reaches ML_MB. In multi-component systems, it can happen that, although ML_MB is set to the computationally affordable maximum, one species exceeds ML_MB while the other species are not sufficiently sampled and are still far below ML_MB. For that ML_LBASIS_DISCARD=.TRUE. should be set. In that case, the fast sampled species would retain the same number of local reference configurations and the new local reference configurations would replace the old ones. At the same time, new local reference configurations could be added for the slowly-sampled species further improving their accuracy for fitting.

Testing

• Set up an independent test set of random configurations. Then, check the average errors comparing forces, stresses, and energy differences of two structures based on DFT and predicted by machine-learned force fields.

• If you have both, ab-initio reference data and a calculation using force fields, check the agreement of some physical properties. For instance, you might check the relaxed lattice parameters, phonons, relative energies of different phases, the elastic constant, the formation of defects, etc.

• Plot blocked averages to monitor some characteristic values (volume, pressure, etc.).

Application

The following things need to be considered when running only the force field (ML_ISTART=2):

• Set the ab-initio parameters to small values. VASP cannot circumvent the initialization of KS orbitals although they are not used during the molecular dynamics run with machine learning.
• Monitor the Bayesian error estimates (BEEF). An increase of this value indicates extrapolation of the force field. In that case, the current structure was not contained within the training structures and needs to be included.

Example

Sample input for learning of liquid water in the NpT ensemble at 0.001 kB using a temperature ramp.

INCAR:

ENCUT            = 700 #larger cutoff
LASPH            = .True.
GGA              = RP
IVDW             = 11
ALGO             = Normal
LREAL            = Auto

ISYM             = 0

IBRION           = 0
MDALGO           = 3
ISIF             = 3
POTIM            = 1.5
TEBEG            = 200
TEEND            = 500
LANGEVIN_GAMMA   = 10.0 10.0
LANGEVIN_GAMMA_L = 3.0
PMASS            = 100
PSTRESS          = 0.001
NSW              = 20000

POMASS           = 8.0 16.0

ML_LMLFF         = .TRUE.
ML_ISTART        = 0

• ENCUT: A larger plane-wave cut-off is used to accommodate possible changes in the lattice parameters, because an NpT ensemble is used (ISIF=3).
• POMASS: Since this structure contains Hydrogen, the mass of Hydrogen is increased by a factor of 8 to be able to use larger integration steps POTIM. Without this one possibly needs to use integration steps of POTIM<0.5 hugely increasing the computation time.
• Here GGA=RP together with IVDW=11 is used which gives a good electron exchange and correlation description for liquid water.

ICONST:

LA 1 2 0
LA 1 3 0
LA 2 3 0
LR 1 0
LR 2 0
LR 3 0
S  1  0  0  0  0  0 0
S  0  1  0  0  0  0 0
S  0  0  1  0  0  0 0
S  0  0  0  1 -1  0 0
S  0  0  0  1  0 -1 0
S  0  0  0  0  1 -1 0

• Since a liquid in the NpT ensemble is simulated here, the ICONST file ensures that the lattice parameters are allowed to change to accommodate the pressure, but the length ratio and angles between the lattice parameters remain constant. This prevents unwanted deformations of the cell.

POSCAR:

Click to show POSCAR

H2O_liquid
   1.00000000000000
    12.5163422232076691    0.0000233914035418    0.0000148478021513
     0.0000000000114008   12.5162286489880472    0.0000199363611203
     0.0000000000209813    0.0000000000005105   12.5176610723470780
   H    O
   126    63
Direct
  0.2282617284551465  0.0100328590137529 -0.1126387890656106
  0.9746403004006459 -0.2476460083611154 -0.2607428157584675
  0.5495157277709571  0.8457364197593650 -0.2477873147502692
  0.8285605776747957  1.3957130438711647  0.3236429564827718
  0.7772914822330327  0.4827858883979471  0.6904243173615018
  0.0577768259920047  0.2223168123471880 -0.7608749959673696
  0.9446580715027482  1.1212973211581765  0.3550426042339572
  0.8506873790066947  0.1718425528358722  0.6288341575238712
  0.6762596340888892  0.6505044169314104  0.2894195166948972
  0.5611370443226182 -0.0333524123727857  0.5214208317960167
  0.6816550720303126 -0.1211211829857703  0.4073898872723471
  0.9980109015831524  0.4469736864199069  0.7701748771760492
  0.6678832112330954  0.5234479361650100  0.1656392748166443
  0.5040346446185426  0.5390736385800624  0.3470193329922442
  0.6410360744431883  1.2034330133853826 -0.5204809500538871
  0.5009140032853824  1.0194465602602765  0.0680968735186743
  1.1286687923693957  0.4815796673077014  0.1056405447614227
  1.3281242572016398 -0.0586744504576348  1.2791126768723411
  1.2745979045721432  0.6605001257033906  0.1708686731589134
  0.4889175843208496  0.3992133071729653  0.6662361557283188
  1.1680688935402925  0.7448174915883062  0.4840737703429457
  0.5441535549963540  1.2562238170486451 -0.1933215921435651
  0.7539782822013665  0.4393165162255908 -0.1111210880770900
  0.7158370742172643  0.2516648581738293  0.0129481804279206
  0.2713582658190841  0.2279864583332417 -0.2165119651431964
  0.9024539921023629 -0.1184662408708287  0.6213800486657953
  0.4615161508482398  0.2475213172787736  0.4504737358928211
  1.0118559400607643  0.7424282505541469  0.0746984790656740
  0.2903967612053814  0.3755361842352651  0.5760967580335238
  0.3231287130417146  0.7657698148287657 -0.4355073700974863
  1.0376988097955901  0.0758439375796752 -0.0755636247212518
  0.3490021766854268 -0.0144512406004137 -0.1286563387493205
  0.9105647459905236  0.7180137269788829 -0.1630338422998813
  0.6217984736501840  0.7636375746785418 -0.2985814512057716
  0.7745581203120666  1.3708044347688073  0.2161898767275624
  0.6604329281507487  0.4588369178206191  0.6638505715678867
  0.9367092142161492  0.2566478031322914 -0.7657152701827817
  0.9210696992439242  1.0100086011945200  0.3831186344742445
  0.7198461947247682  0.1832700676815498  0.6289634217232680
  0.5794490968641994  0.6650526418110994  0.2084878611072036
  0.4451295011889302  0.0227193097626150  0.5285299460037345
  0.6493078638087474 -0.2119508709082261  0.4952750816523580
  0.9786031188935814  0.5691499073939285  0.7498421879775161
  0.7284271721290199  0.4873101999963645  0.0606006569966631
  0.4910977185777734  0.5607404559463554  0.4688446654579101
  0.5685724756690831  1.1303057766954432 -0.4520626434287254
  0.5834889098964630  0.9606882347596553  0.0036536368035990
  1.0401204359334022  0.5623696717124362  0.0540990885930118
  1.2824173065014235  0.0145062237175715  1.3666813391539134
  0.3486617682267537 -0.2934149709168444  0.0822130144717180
  0.5730104678470570  0.3084776512554136  0.6220956625895938
  0.0696111366994306  0.7429990748207962  0.4037397615014190
  0.5502677722150517  1.2295680823859727 -0.0773553830031266
  0.6629391487219132  0.5328361705119534 -0.1150519950062741
  0.6250848388543612  0.3083123187101773  0.0765665590910336
  0.3662802395551557  0.2702906914452067 -0.1383165019423200
  0.9736705556543800 -0.1799052283389148  0.5343666577034214
  0.4295248327300012  0.3704736742659817  0.4332641348308674
  0.8980973959825628  0.6990554008415506  0.0343927673672955
  0.2875819013957733  0.4057639685103899 -0.3043930746820226
  0.2339822436285078  0.7745846329456394  0.6458551118383669
  1.0595055035190402 -0.0564894402119362 -0.0902725095487327
  0.8934974071042586  0.3290512561302191  0.8603972804418396
  0.5553026810346389  0.6918749861685528  0.8648052870098396
  0.7595162123757241  0.2391418457892084  0.3402576351144293
  0.1473261899861980  0.3709222233120330  0.4682213790034302
  0.1421840618221771  0.3140746572683427 -0.1121762131537217
  1.3389241568069978  0.3988616347426453  0.1635703018210843
 -0.2448915061544370  0.7563953018862059 -0.0736150977487566
  0.7590706624915531  0.4910146399954628  0.4684780730777085
  0.7950571409085634  0.7192143646959017  0.5985905369710599
  0.1316279824003455  1.0999687910648197  0.7533188747497124
  0.1904139474335156  0.7791943520426338  0.0571106523349340
  1.2220229066248534  0.3192108772536086  0.2369051680927172
  0.3612775881033622  0.0855989478292645  0.1403208309917672
 -0.1361272699805649  0.6820997653177969  0.2354821840318570
  0.4087521084198726  0.5912825002582747  0.6358439098196149
  0.1239762404674222  0.7546282143520640 -0.2004037475678275
  0.3254524437469295  0.5629691201597067  0.3724966107408161
  0.4753895829795802  1.0167551557396182  0.7120469261102015
  0.2608638376650217  1.0575489302906138  0.5689964057513199
  0.1643499778763993  0.9878520821198175  0.2274680280884254
  0.5044272836232667 -0.1889898057206633  1.0969173862764161
  1.0108484544264800  0.2499932639019371 -0.0323289029244656
  1.4604847395188030 -0.1857921072604787  0.3648781664672482
 -0.0676389676130162 -0.0295362893506241  0.7871165868504495
  0.4846115199200384  0.2254773218591808  0.1655080485768635
  0.7546930244801831  0.9283849256193616  0.8541595795735338
  0.9706434056979190  1.1154826414004460  0.5267461552592998
 -0.0861615702697154 -0.1809840616227028 -0.6553434728259054
  0.8442013982186719 -0.0307048052283226  0.1425354846866949
  0.6887583721043200  1.0654555145745237  0.2683125737537906
  1.0027728188337521  0.5023071178777798 -0.4225836976328659
  1.2932985504962016  1.5692646782719462  0.9368592413035413
  0.4716460351076925  0.6993549392273799  0.6601847017954563
  0.2065050455598290  0.8340729505249687 -0.1549365584796285
  0.7134717637166987  0.6306375489985552  0.5979355450208014
  0.1305819547597963  1.1628983978276421  0.6489352069792226
  0.1272197155625575  0.8779790277321273  0.1016609192978390
  1.2490179100185559  0.1997381130828568  0.2661804901290689
  1.3538940004316671  0.0865346934520785  0.0162268012094167
 -0.1648144254795892  0.6328837747686877  0.3517458960703262
  1.3576963330025944 -0.2535471527532498  0.3451642885788545
 -0.1512707063199035  0.0447723975378184  0.7370562480777335
  0.2082920817694131  0.6238194842808575  0.3627405505637077
  0.4818735663404834  0.0797305025898344  0.8149171190132681
  0.2714920258235731  0.9437115667773756  0.5398585008814204
  0.0598987571605861  1.0109519535694200  0.1622926257298793
  0.5118223005328099 -0.2906673876063635  1.0219508170746381
  0.9862800303912808  0.1828001523416312  0.0677466130856736
  1.0595449212229817  0.5431076873367398 -0.5303300708777712
  1.2934388789888798  0.6286357417906868 -0.1682875581053126
  0.4618116975337169  0.2958921133995223  0.2670334121905841
  0.7539636581184406  0.9360985551615451 -0.0248108921725196
  0.9998082474973725  1.2364748213827927  0.5458537302387204
  0.0084172701408917 -0.0989295133906621 -0.6906681930981559
  0.9033157610523457 -0.1303930279825006  0.1228072425414686
  0.6604461112340703  0.9892487041136045  0.1825505778817879
  0.7885276375808787  0.6294686108635517 -0.0737926736153585
  0.8840546243663174  0.5053739463625377  0.4526376410385395
  0.8074749932462770  0.2947711469591280  0.7787234411725377
  0.4632367138215856  0.6097289940035490 -0.1145492866143238
  0.7775247539743841  0.1357560792893380  0.4055163611357055
  0.2117515661833950  0.2832304177268588  0.4122050502626490
  0.0768107057290735  0.4027427851525467 -0.0515166562421230
  1.2669405505626230  0.4880120983162565  0.2202021018146102
  0.2919481531025963 -0.0097036832216508 -0.0729957055081244
  0.9840898695695925  0.7046088238612841 -0.1980300785209053
  0.5582639462588442  0.7673812911725254 -0.2587733472825737
  0.8220678952661906  1.3361683524558097  0.2699860947274584
  0.7257118638315225  0.4999486906307656  0.6412374880809832
 -0.0159466690459744  0.1935938619023044 -0.7768095097490648
  0.9155392077434708  1.0805930191162569  0.4138690591165022
  0.7862174758070717  0.1816706702550143  0.6732485622988889
  0.6132430910865457  0.6183045290387048  0.2587122784691759
  0.5240798045171384  0.0270658373485661  0.5490772798003927
  0.6227258931836714 -0.1513468939644967  0.4514026249947363
  0.9638867643770986  0.4954513053854325  0.7212510085139069
  0.7159100053950270  0.4678155943640417  0.1349439087134111
  0.4582333315581760  0.5168500155232567  0.4094860848574138
  0.6020128307710225  1.2064430441579375 -0.4506555458643959
  0.5521951499401644  0.9590467759911693  0.0741168885795418
  1.0781674762106039  0.4954947302196762  0.0441857869962515
  1.2877834938552375  0.0081337644237061  1.2888612376304034
  1.2732518381606885 -0.3103063836930492  0.0984742851109190
  0.5595086990259246  0.3696506726448117  0.6743217671307982
  0.1240887034225702  0.6960193789405823  0.4337932939025890
  0.5086138696669937  1.2114646205434219 -0.1402693575758740
  0.7313300345574206  0.5088192316865796 -0.0848414107423346
  0.6392500541546888  0.2452966478859945  0.0290217369836307
  0.2906220813433669  0.2834501467738138 -0.1612157326655933
  0.9265368908511590 -0.1886857109185944  0.5950530730285820
  0.4191322585983637  0.2968514680208339  0.4065358381730697
  0.9503223312345728  0.6924078287564821  0.0976010227803059
  0.3171226540194806  0.4277726129695098  0.6291827895026040
  0.2523597102929802  0.7992029127084535 -0.4251410697001895
  1.0542894643082081  0.0098095875712209 -0.1254405527744111
 -0.1850276732646079  0.7064002231521372 -0.0809385398102708
  0.8146436675316787  0.5091462597700946  0.4152356140927696
  0.8203699138320668  0.3369968354028824  0.8455921310438892
  0.5350509729728494  0.6295527668603674  0.9102304780657455
  0.7193764908855955  0.1838347476185205  0.3819141293957220
  0.1910314352006382  0.3094472630165150  0.4823838977521944
  0.0687276874475614  0.3407534564140682 -0.0961793949793184
  1.2668203814128003  0.4259424135404398  0.1731136054217358
  0.4280856307534187  0.6584589779898570  0.6012619513268567
  1.1963611411889725  0.7804022094739607 -0.2110274995492418
  0.7214250257605557  0.7065604538172952  0.5794991635695482
  0.1776849231487917  1.1234852797096138  0.6937893559514705
  0.1285406853584958  0.8283735895779946  0.0360212378784548
  1.1982000164502744  0.2527276897017764  0.2755163953762200
  0.3971884946158640  0.1135585073114126  0.0762033607013268
 -0.1677109438487009  0.6976010251448760  0.3070009760429893
  1.3843291659064216 -0.1806544740790267  0.3487638347163066
 -0.1370877275115541 -0.0294965108434674  0.7526972827056088
  0.2742057504147322  0.5976400628879622  0.3238891214955297
  0.4681381611246405  1.0080818685930206  0.7875962423618043
  0.2988391245755818  1.0128379546679014  0.5215141172374251
  0.0979325070909129  0.9559351747734792  0.2036472418484847
  0.4871098095650768 -0.2661593993271190  1.0958159235212488
  0.9840996652256983  0.1761359392656111 -0.0086227132193279
  1.0181722221064600  0.4832974111083591 -0.4993793874483681
  1.3336737594231565  0.5733445036683216  0.8701294276086065
  0.4805509314794579  0.2981571227457179  0.1930037183242462
  0.7146125697156993  0.8998617569525493  0.9145452976881076
  0.9916627840023351  1.1683363103812550  0.5804316669886708
 -0.0389136332191330 -0.1241670083541440 -0.6326131437048044
  0.8956869974284227 -0.0586980011006573  0.0867714766274296
  0.7097227556462733  0.9934862114531017  0.2391419679113634

Related articles

Machine-learned force fields, Ionic minimization, Molecular dynamics, Machine learning force field calculations: Basics