FAQ

I can not compile the parallel version of VASP under LINUX?

Mind that VASP will generally not link correctly to mpi versions compiled with g77/f77, since g77/f77 append two underscores to external symbols already containing one underscore (i.e. MPI_SEND becomes mpi_send__). The portland group compiler however appends one underscore. Although the pgf90 compiler has an option to work around this problem, we yet faild to link against mpi libraries generated for g77/f77. Hence you must compile mpi (mpich and/or lam) yourself. This is really easy and simple, if the machine has been set up properly (have a look at our makefiles). If the compilation of mpich and/or lam fails, VASP will almost certainly not work in parallel on your machine, and we strongly urge you to reinstall LINUX.

Why is the cohesive energy much large than reported in other papers?

Several reasons can be responsible for this:

First, VASP calculates the cohesive energy with respect to a spherical non spin-polarised atom. One should however calculate the cohesive energy with respect to a spin polarised atom. These corrections are usually called (atomic) spin-polarisation corrections, and they must be subtracted manually from the calculated cohesive energy calculated by VASP.

Second, many older calculations report too small cohesive energies, since basis sets were often insufficient. It is now well accepted that the local density approximation overestimates the cohesive energy significantly in many cases.

Which k-points should I use?

For metallic system, k-point convergence is usually a critical issue. There are a few general hints which might be helpfull:

For hexagonal cells, Gamma centered k-point grids converge much faster than other grids. In fact, most meshes that do not include the $\Gamma$ point break the symmetry of the hexagonal lattice! Even with increasing grid densities the wrong results might be obtained.

Up to divisions of 8 (i.e. $8\times8\times1$ for a surface) even Monkhorst Pack grids which do not contain the Gamma point, perform better than odd Monkhorst Pack grids (this does not apply to hexagonal cells, see above). In other words one obtains better converged results with even grids.

For adsorbates on surfaces, it is sometimes feasable to use only the k-points of the high symmetry Brillouin zone, even if the adsorbate breaks the symmetry. These k-point grids can be generated by running VASP with a POSCAR for which all adatoms have been removed. The resulting IBZKPT file can be copied to KPOINTS. For convenicene, the following k-point grids can be used for hexagonal cells:

Gamma centered 2x2
Automatically generated mesh
       2
Reciprocal lattice
    0.00000000000000    0.00000000000000    0.00000000000000             1
    0.50000000000000    0.00000000000000    0.00000000000000             3

Gamma centered 3x3
Automatically generated mesh
       3
Reciprocal lattice
    0.00000000000000    0.00000000000000    0.00000000000000             1
    0.33333333333333    0.00000000000000    0.00000000000000             6
    0.33333333333333    0.33333333333333    0.00000000000000             2    

Gamma centered 4x4
Automatically generated mesh
       4
Reciprocal lattice
    0.00000000000000    0.00000000000000    0.00000000000000             1
    0.25000000000000    0.00000000000000    0.00000000000000             6
    0.50000000000000    0.00000000000000    0.00000000000000             3
    0.25000000000000    0.25000000000000    0.00000000000000             6  

Gamma centered 5x5
Automatically generated mesh
       5
Reciprocal lattice
    0.00000000000000    0.00000000000000    0.00000000000000             1
    0.20000000000000    0.00000000000000    0.00000000000000             6
    0.40000000000000    0.00000000000000    0.00000000000000             6
    0.20000000000000    0.20000000000000    0.00000000000000             6
    0.40000000000000    0.20000000000000    0.00000000000000             6  

Gamma centered 6x6
Automatically generated mesh
       7
Reciprocal lattice
    0.00000000000000    0.00000000000000    0.00000000000000             1
    0.16666666666667    0.00000000000000    0.00000000000000             6
    0.33333333333333    0.00000000000000    0.00000000000000             6
    0.50000000000000    0.00000000000000    0.00000000000000             3
    0.16666666666667    0.16666666666667    0.00000000000000             6
    0.33333333333333    0.16666666666667    0.00000000000000            12
    0.33333333333333    0.33333333333333    0.00000000000000             2

For cubic surface cells, the following k-points can be used:

Monkhorst Pack: 2x2x1
       1
Reciprocal lattice
    0.25000000000000    0.25000000000000    0.00000000000000             4

Monkhorst Pack: 4x4x1
       3
Reciprocal lattice
    0.12500000000000    0.12500000000000    0.00000000000000             4
    0.37500000000000    0.12500000000000    0.00000000000000             8
    0.37500000000000    0.37500000000000    0.00000000000000             4

Monkhorst Pack: 6x6x1
       6
Reciprocal lattice
    0.08333333333333    0.08333333333333    0.00000000000000             4
    0.25000000000000    0.08333333333333    0.00000000000000             8
    0.41666666666667    0.08333333333333    0.00000000000000             8
    0.25000000000000    0.25000000000000    0.00000000000000             4
    0.41666666666667    0.25000000000000    0.00000000000000             8

Monkhorst Pack: 8x8x1
      10
Reciprocal lattice
    0.06250000000000    0.06250000000000    0.00000000000000             4
    0.18750000000000    0.06250000000000    0.00000000000000             8
    0.31250000000000    0.06250000000000    0.00000000000000             8
    0.43750000000000    0.06250000000000    0.00000000000000             8
    0.18750000000000    0.18750000000000    0.00000000000000             4
    0.31250000000000    0.18750000000000    0.00000000000000             8
    0.43750000000000    0.18750000000000    0.00000000000000             8
    0.31250000000000    0.31250000000000    0.00000000000000             4
    0.43750000000000    0.31250000000000    0.00000000000000             8
    0.43750000000000    0.43750000000000    0.00000000000000             4

Question Why is convergence to the ionic groundstate so slow?

In general convergence depends on the eigenvalue spectrum of the Hessian matrix (second derivative of the energy with respect to positions). Roughly speaking the number of steps equals

${\displaystyle N = \sqrt{ \frac{ \epsilon_{\rm max}}{ \epsilon_{\rm min}}} }$

if a conjugate gradient, or Quasi-Newton algorithm is chosen. If a good structural start guess exists, the best convergence can be obtained with IBRION=1 and NFREE (number of degrees of freedon) set to a reasonable value. If the initial start guess is bad, it is sometimes required to use the safer conjugate gradient algorithm.

A very important point concerns the required accuracy of the electronic degrees of freedom. If the eigenvalue spectrum of the Hessian matrix is small, EDIFF can be rather large (EDIFF=1E-3). However if the eigenvalue spectrum is broad, EDIFF must be set to a smaller value EDIFF=1E-5, since otherwise the slowly varying degrees of freedom can not be accurately determined in the Hessian matrix. If no convergence is observed for IBRION=1, try to decrease EDIFF.

== I see unphysical oszillations and negative values for the chargedensity in the vacuum. Is VASP not able to give reliable results in the vacuum? ==

VASP gives reliable results, but things are complicated by several issues:

Avoid, ISMEAR>0, when considering the wavefunctions in the vacuum. It can cause negative occupancies close to the Fermi-level, and since states at the Fermi-level decay slowest in the vacuum, the charge density in the vacuum might be negativ (energies are not effected by this, since the wavefunctions in the vacuum do not contribute significantly to the energy).
The charge density of selfconsistent calculations might have negative values in the vacuum, since the mixer is very insensitive to the charge density in the vacuum. It is better to set LPARD=.TRUE. and call VASP a second time. The generated CHGCAR file contains the chargedensity calculated directly from the wavefunctions.
In VASP, pseudo charge density components from unbalanced lattice vectors are set to zero: although the charge density is initially calculated in real space and therefore positive definite, it is modified then in reciprocal space, and Fourier transformed back to real space. The final charge density has small oscillations in the vacuum. To avoid this problem, use FFT grids that avoid wrap around errors (PREC=Accurate). The problem can also be reduced by increasing the energy cut off.
Ultrasoft pseudopotentials require a second support grid. In VASP.4.4.4 and older version, charge density components from unbalanced lattice vectors are also zeroed on the second support grid, causing additional small oscillations in the vacuum. This problem is removed in VASP.4.5 and in VASP.4.4.5. In VASP.4.4.5 the flag -DVASP45 must be specified in the CPP line of the makefile before compiling the VASP code. Total energies might however change by a fraction of a meV.

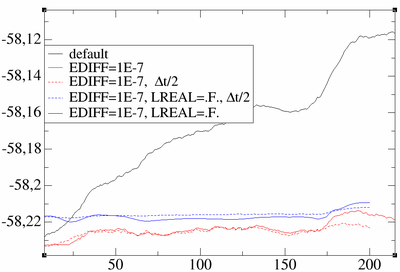
I am running molecular dynamics and observe a large drift in the total energy, that should be conserved.

Three reasons can hamper the energy conservation in VASP.

First the electronic convergence might not be sufficiently tight. It is often necessary to decrease the tolerance to $10^{-6}$ or $10^{-7}$ to obtain excellent energy conservation. Alternatively NELMIN can be set to values around 6.
The second reason is an insufficiently accurate real space projection. This usually causes a slightly spiky and discontinuous total energy. If you observe such a behavior, you have to improve ROPT, or set LREAL=.FALSE.
Finally, consider reducing the time step.

The following graph illustrates the behavior for a small liquid metallic system (Ti). It shows the energy conservation for a liquid metallic system for various settings. Please mind, that reducing ROPT from -0.002 to -.0005 (LREAL=.A.) had the same effect as using LREAL=.FALSE.