Biased molecular dynamics

The probability density for a geometric parameter ξ of the system driven by a Hamiltonian:

{\displaystyle H(q,p) = T(p) + V(q), \; }

with T(p), and V(q) being kinetic, and potential energies, respectively, can be written as:

{\displaystyle P(\xi_i)=\frac{\int\delta\Big(\xi(q)-\xi_i\Big) \exp\left\{-H(q,p)/k_B\,T\right\} dq\,dp}{\int \exp\left\{-H(q,p)/k_B\,T\right\}dq\,dp} = \langle\delta\Big(\xi(q)-\xi_i\Big)\rangle_{H}. }

The term $\langle X \rangle_H$ stands for a thermal average of quantity X evaluated for the system driven by the Hamiltonian H.

If the system is modified by adding a bias potential $\tilde{V}(\xi)$ acting on one or multiple selected internal coordinates of the system ξ=ξ(q), the Hamiltonian takes a form:

{\displaystyle \tilde{H}(q,p) = H(q,p) + \tilde{V}(\xi), }

and the probability density of ξ in the biased ensemble is:

{\displaystyle \tilde{P}(\xi_i)= \frac{\int \delta\Big(\xi(q)-\xi_i\Big) \exp\left\{-\tilde{H}(q,p)/k_B\,T\right\} dq\,dp}{\int \exp\left\{-\tilde{H}(q,p)/k_B\,T\right\}dq\,dp} = \langle\delta\Big(\xi(q)-\xi_i\Big)\rangle_{\tilde{H}} }

It can be shown that the biased and unbiased averages are related via a simple formula:

{\displaystyle P(\xi_i)=\tilde{P}(\xi_i) \frac{\exp\left\{\tilde{V}(\xi)/k_B\,T\right\}}{\langle \exp\left\{\tilde{V}(\xi)/k_B\,T\right\} \rangle_{\tilde{H}}}. }

More generally, an observable $\langle A \rangle_{H}$ :

{\displaystyle \langle A \rangle_{H} = \frac{\int A(q) \exp\left\{-H(q,p)/k_B\,T\right\} dq\,dp}{\int \exp\left\{-H(q,p)/k_B\,T\right\}dq\,dp} }

can be expressed in terms of thermal averages within the biased ensemble:

{\displaystyle \langle A \rangle_{H} =\frac{\langle A(q) \,\exp\left\{\tilde{V}(\xi)/k_B\,T\right\} \rangle_{\tilde{H}}}{\langle \exp\left\{\tilde{V}(\xi)/k_B\,T\right\} \rangle_{\tilde{H}}}. }

Simulation methods such as umbrella sampling^[1] use a bias potential to enhance sampling of ξ in regions with low P(ξ_i) such as transition regions of chemical reactions. The correct distributions are recovered afterwards using the equation for $\langle A \rangle_{H}$ above.

A more detailed description of the method can be found in Ref.^[2]. Biased molecular dynamics can be used also to introduce soft geometric constraints in which the controlled geometric parameter is not strictly constant, instead it oscillates in a narrow interval of values. The bias potentials are supported both the NVT and NpT MD simulations regardless of the particular thermostat and/or barostat setting. Different types of potentials can be freely combined.

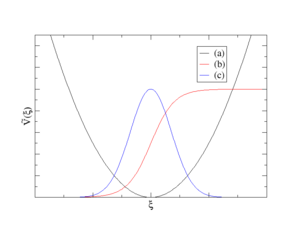
Supported types of bias potentials

Presently, the following types of bias potential are supported:

Harmonic potential (see curve (a) on the plot above)

{\displaystyle \tilde{V}(\xi_1,\dots,\xi_{M}) = \sum_{\mu=1}^{M}\frac{1}{2}\kappa_{\mu} (\xi_{\mu}(q)-\xi_{0,\mu})^2 \; }

where the sum runs all ( $M$ ) coordinates the potential acts upon, which are defined in the ICONST-file by setting the status to 8. The parameters of the potential, $\kappa$ (force constant) and $\xi_0$ (minimum of potential), are defined, respectively, via the keywords SPRING_K and SPRING_R0 in INCAR. Optionally, it is also possible to change the value of $\xi_{0,\mu}$ every MD step at a constant rate defined via parameter SPRING_V. Note that the number of items defined via SPRING_K, SPRING_R0, and SPRING_V must be equal to $M$ , otherwise the calculation terminates with an error message. This form of bias potential is employed in several simulation protocols, such as the umbrella sampling^[1], umbrella integration, or steered MD, and is useful also in cases where the $\xi_{\mu}$ values need restrained.

Fermi function (see curve (b) on the plot above)

{\displaystyle \tilde{V}(\xi_1,\dots,\xi_{M}) = \sum_{\mu=1}^{M}\frac{A_{\mu}}{1+\text{exp}\left [-D_{\mu}\frac{\xi(q)}{\xi_{0,\mu}} -1 \right ]} \; }

where the sum runs all ( $M$ ) coordinates the potential acts upon, which are defined in the ICONST-file by setting the status to 4.

FBIAS_A FBIAS_D FBIAS_R0

Gauss function (see curve (b) on the plot above)

{\displaystyle \tilde{V}(\xi_1,\dots,\xi_{M}) = h\,\sum_{\mu=1}^{M}\text{exp}\left [-\frac{(\xi(q)-\xi_0)^2}{2w^2} \right ], \; }

Andersen thermostat

For a biased molecular dynamics run with Andersen thermostat, one has to:

Set the standard MD-related tags: IBRION=0, TEBEG, POTIM, and NSW
Set MDALGO=1 (MDALGO=11 in VASP 5.x), and choose an appropriate setting for ANDERSEN_PROB
In order to avoid updating of the bias potential, set HILLS_BIN=NSW
Define collective variables in the ICONST-file, and set the STATUS parameter for the collective variables to 5
Define the bias potential in the PENALTYPOT-file

Nose-Hoover thermostat

For a biased molecular dynamics run with Nose-Hoover thermostat, one has to:

Set the standard MD-related tags: IBRION=0, TEBEG, POTIM, and NSW
Set MDALGO=2 (MDALGO=21 in VASP 5.x), and choose an appropriate setting for SMASS
In order to avoid updating of the bias potential, set HILLS_BIN=NSW
Define collective variables in the ICONST-file, and set the STATUS parameter for the collective variables to 5
Define the bias potential in the PENALTYPOT-file

The values of all collective variables for each MD step are listed in the REPORT-file, check the lines after the string Metadynamics.

References

↑ ^a ^b G. M. Torrie and J. P. Valleau, J. Comp. Phys. 23, 187 (1977).
↑ D. Frenkel and B. Smit, Understanding molecular simulations: from algorithms to applications, Academic Press: San Diego, 2002.

[Torrie77-1] G. M. Torrie and J. P. Valleau, J. Comp. Phys. 23, 187 (1977).

[FrenkelSmit-2] D. Frenkel and B. Smit, Understanding molecular simulations: from algorithms to applications, Academic Press: San Diego, 2002.

[1]

[2]