Charge sloshing

Fig. 1: A handwaving illustration of charge sloshing.

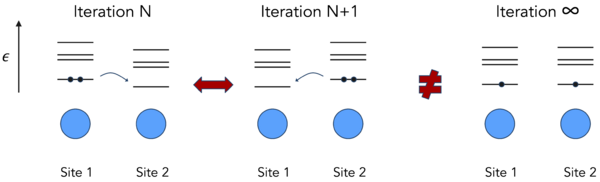
A very handwaving illustration of the phenomenon of charge sloshing during the electronic optimization is shown in Fig. 1:

• Suppose we have a system with two chemically identical sites (Site 1 and 2), and suppose that in step N of the electronic optimization the situation is as follows:

At the beginning of iteration N, Site 1 is occupied by 2 electrons, Site 2 is empty. After the refinement of the one-electron orbitals, however, the lowest eigenstate associated with Site 2 lies below the occupied state at Site 1.

• In step N+1 the situation is reversed: the two electrons that were on Site 1 now are on Site 2, and after the refinement of the one-electron orbitals the lowest lying state at Site 1 will lie below the occupied state at Site 2.

• In subsequent steps the situation will bounce back-and-forth between the two aforementioned states, without ever reaching the "groundstate" depicted on the right in Fig. 1, where both Site 1 as well as Site 2 are occupied by a single electron.

A bit more mathematical explanation for the occurrence of charge sloshing goes as follows:

• Consider a metal, with "free electron"-like states at the Fermi-level, and consider a very large supercell, in which a single k-point suffices to sample the Brillouin zone, and hence all states are folded back to this point in the Brillouin zone.

The state just below the Fermi-level is approximately given by $\psi_n = e^{i ({\bf k}_F-\delta {\bf k}){\bf r}}$, and the one above the Fermi-level by $\psi_m = e^{i ({\bf k}_F+\delta {\bf k}) {\bf r}}$. The former is occupied and the latter is not.

• During the electronic optimization, orbitals $\psi_n$ and $\psi_m$ will hybridize. This happens because the gradient of the total energy with respect to the orbitals has a so-called subspace rotational component:

$| s_n \rangle = \sum^N_{m=1} \frac{1}{2} {\bf H}_{nm} (f_n - f_m) \hat{S} \vert \psi_m \rangle$

where $\{ f_i | i=1,..,N \}$ are the partial occupancies, and

${\bf H}_{nm}=\langle \psi_m \vert \hat{H} \vert \psi_n \rangle$

is the Hamiltonian expressed within the subspace spanned by the current orbitals $\{ \psi_i | i=1,..,N \}$.

A suitable search direction along the subspace rotational part of the gradient is given by a small unitary rotation between orbitals $\psi_n$ and $\psi_m$:

$|\psi'_n \rangle = | \psi_n \rangle + \Delta | \psi_m \rangle \qquad |\psi'_m \rangle = | \psi_m \rangle - \Delta | \psi_n \rangle$

where $\Delta$ denotes the stepsize.

• The aformentioned change in the orbitals leads to a long-wavelength change in the charge density:

$\delta\rho({\bf r})=2 \Delta {\rm Re}\, e^{i 2 \delta{\bf k}\cdot{\bf r}}$

and the consequent change in the Hartree potential due to this long-wavelength change in the density is given by:

$\delta V_{\rm H}({\bf r})=2 \Delta \frac{4 \pi e^2}{ | 2\delta {\bf k}|^2}{\rm Re} \,e^{i 2 \delta{\bf k}\cdot{\bf r}}.$

The factor $1/|\delta {\bf k}|^2$ in the above is in fact the principal origin of charge sloshing: a long-wavelength change in the charge density leads to a strongly amplified change in the electrostatic potential.

• In our example, the smallest possible $|\delta {\bf k}|$ is proportional to L, the maximum extent of the supercell:

$|\delta {\bf k}| \propto 2 \pi / L$,

and thus the response in the potential increases with L², the square of the maximum extent of the supercell.

Consequently, the maximum stable step size in a direct optimization algorithm decreases inversely proportional to the square of the maximum extent of the supercell ($\Delta = 1/L^2$).

The reasoning above elucidates two important aspects of charge sloshing:

• Metals and systems with a small gap are more prone to charge sloshing than wide-gap insulators.

• Problems due to charge sloshing increase with increasing (super)cell size.

To prevent charge sloshing VASP uses density mixing in the self-consistency cycle.

Related tags and articles

ICHARG, AMIX, BMIX, AMIX_MAG, BMIX_MAG, Troubleshooting electronic convergence