Category:Pseudopotentials: Difference between revisions
(Created blank page) |
No edit summary |
||
| Line 1: | Line 1: | ||
[[File:Sketch Pseudopotentials.png|300px|right|Sketch of a pseudopotential and pseudowavefunction]] | |||
'''Pseudopotentials''', or effective potentials, are well-behaved potentials that replace the ionic potentials that are diverging near the nuclei. As a result, [[Pseudopotential_basics|the pseudopotential approach]] significantly speeds up [[Electronic_minimization|electronic structure calculations]] and makes the simulation of more materials feasible. | |||
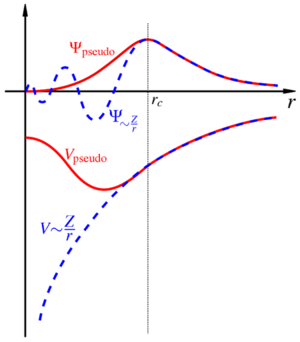
For periodic systems it is convenient to use a plane-wave basis, however, describing the oscillations near the nuclei (nodal features) would necessitate an excessively high number of plane waves. Instead, one introduces pseudopotentials and resulting pseudo orbitals. These are identical to the true ionic potentials and orbitals outside a specific radius, but the pseudo orbitals contain no nodal features. Thus, the cell-periodic part of the pseudo orbitals is suitable to be treated in a plane-wave basis. | |||
An additional approximation taken alongside the pseudopotential method is the ''frozen-core approximation''. Here, the electrons associated with an ion are separated into valence electrons ({{TAG|ZVAL}}) that are assumed to take part in the physical/chemical property of interest and core electrons that are included as screening of the ionic potential in the pseudopotential. | |||
The cell-periodic part of the pseudo orbitals is computed in terms of plane-wave coefficients, or Fourier components, associated with a reciprocal vector <math>\mathbf{G}</math>. The maximum number of Fourier components (and, hence, the computational cost) is determined by the cutoff radius ({{TAG|ENCUT}}). The appropriate value depends on the system and the selected pseudopotential. For a specific atom type, there are [[available pseudopotentials|multiple pseudopotentials available]] that vary in terms of core radius, the number of electrons, their ability to describe excited states, etc. A potential is considered ''soft'' when few Fourier components are sufficient for an accurate representation, and ''hard'' otherwise. | |||
Revision as of 13:12, 12 June 2024
Pseudopotentials, or effective potentials, are well-behaved potentials that replace the ionic potentials that are diverging near the nuclei. As a result, the pseudopotential approach significantly speeds up electronic structure calculations and makes the simulation of more materials feasible.
For periodic systems it is convenient to use a plane-wave basis, however, describing the oscillations near the nuclei (nodal features) would necessitate an excessively high number of plane waves. Instead, one introduces pseudopotentials and resulting pseudo orbitals. These are identical to the true ionic potentials and orbitals outside a specific radius, but the pseudo orbitals contain no nodal features. Thus, the cell-periodic part of the pseudo orbitals is suitable to be treated in a plane-wave basis.
An additional approximation taken alongside the pseudopotential method is the frozen-core approximation. Here, the electrons associated with an ion are separated into valence electrons (ZVAL) that are assumed to take part in the physical/chemical property of interest and core electrons that are included as screening of the ionic potential in the pseudopotential.
The cell-periodic part of the pseudo orbitals is computed in terms of plane-wave coefficients, or Fourier components, associated with a reciprocal vector . The maximum number of Fourier components (and, hence, the computational cost) is determined by the cutoff radius (ENCUT). The appropriate value depends on the system and the selected pseudopotential. For a specific atom type, there are multiple pseudopotentials available that vary in terms of core radius, the number of electrons, their ability to describe excited states, etc. A potential is considered soft when few Fourier components are sufficient for an accurate representation, and hard otherwise.
Subcategories
This category has the following 2 subcategories, out of 2 total.
Pages in category "Pseudopotentials"
The following 5 pages are in this category, out of 5 total.
