Dielectric properties of Si using BSE: Difference between revisions

Revision as of 15:52, 20 November 2017

Overview > Dielectric properties of Si using BSE > Improving the dielectric function > Plotting the BSE fatband structure of Si > List of tutorials

Task

Description: Calculate the dielectric function of Si including excitonic effects by solving the Bethe-Salpeter equation (BSE) on top of GW0.

Input

POSCAR

Si
 5.4300
0.5 0.5 0.0
0.0 0.5 0.5
0.5 0.0 0.5
2
cart
0.00 0.00 0.00 
0.25 0.25 0.25

INCAR

This is the INCAR file for the basic DFT calculation:

System  = Si
PREC = Normal ; ENCUT = 250.0
ISMEAR = 0 ; SIGMA = 0.01
KPAR = 2
EDIFF = 1.E-8

KPOINTS

Automatic
 0
Gamma
 6 6 6 
 0 0 0

Calculation

The workflow of GW0+BSE calculations is given in doall.sh and consists of the following consecutive steps:

"Standard" DFT groundstate calculation.
Obtain virtual orbitals: needs WAVECAR file from step 1.
The GW0 calculation: need WAVECAR and WAVEDER from step 2.
Optional step: use LOPTICS=.TRUE. to plot dielectric function in the independent particle approximation (IPA) using GW0 quasiparticle energies instead of DFT energies.
The BSE calculation: needs WAVECAR from step 3 and WAVEDER from step 2.

Step 1: DFT groundstate calculation

We perform standard DFT calculation using the INCAR.DFT file.

Step 2: Obtain DFT "virtual" orbitals (empty states)

This step uses the INCAR.DIAG file:

System  = Si
PREC = Normal ; ENCUT = 250.0
ALGO = EXACT ; NELM = 1
ISMEAR = 0 ; SIGMA = 0.01
KPAR = 2
NBANDS = 128
LOPTICS = .TRUE. ; LPEAD = .TRUE.
OMEGAMAX = 40

We use exact diagonalization for this step (ALGO=EXACT) and keep 128 bands after diagonalization (NBANDS=128).
With LPEAD=.TRUE. we use an alternative way of computing the derivates of the orbitals with respect to the Bloch wave vectors.
It is important that this calculations needs the orbitals (WAVECAR file) written in step 1.

Step 3: RPA quasiparticles with single-shot GW (G0W0)

This step uses the INCAR.GW0 file:

System  = Si
PREC = Normal ; ENCUT = 250.0
ALGO = GW0  
ISMEAR = 0 ; SIGMA = 0.01 
ENCUTGW = 150 ; NELM = 1 ;  NOMEGA =  50 ;  OMEGATL = 280
KPAR = 2
#NBANDSO=4 ; NBANDSV=8 ; LADDER=.TRUE. ; LUSEW=.TRUE.
NBANDS = 128
NBANDSGW = 12
LWAVE = .TRUE.
PRECFOCK = Normal

We select the G0W0 method by specifying ALGO=GW0 and {TAG|NELM}}=1.
The energy cut off for the response function is select by ENCUTGW.
The number of point used in the frequency integration is given by NOMEGA.
Use the same number of bands (NBANDS) as in step 2, otherwise the WAVEDER file is not read correctly.
The quasiparticle energies are calculated for the first few bands given by NBANDSGW.
It is important that this calculation needs the orbitals (WAVECAR file) and the derivatives of the orbitals with respect to the Bloch vectors (WAVEDER file).
The quasiparticle energies can be found in the OUTCAR file (saved as OUTCAR.GW0 in this example):

  QP shifts <psi_nk| G(iteration)W_0 |psi_nk>: iteration 1
for sc-GW calculations column KS-energies equals QP-energies in previous step
and V_xc(KS)=  KS-energies - (<T + V_ion + V_H > + <T+V_H+V_ion>^1  + <V_x>^1)
 
k-point   1 :       0.0000    0.0000    0.0000
 band No.  KS-energies  QP-energies   sigma(KS)   V_xc(KS)     V^pw_x(r,r')   Z            occupation

Step 4 (optional): Plot IPA dielectric function using GW0 quasiparticle energies

This step uses the INCAR.NONE file:

System  = Si
PREC = Normal ; ENCUT = 250.0
ALGO = Nothing ; NELM = 1
ISMEAR = 0 ; SIGMA = 0.01
KPAR = 2
NBANDS = 128
LWAVE = .FALSE.
LOPTICS = .TRUE. ; LPEAD = .TRUE.
OMEGAMAX = 40

By specyfing ALGO=Nothing we do nothing except reading the WAVECAR file.
Using LOPTICS=.TRUE. and LPEAD=.TRUE. we compute the dielectric function in the IPA.

Step 5: The BSE calculation

This step uses the INCAR.BSE file:

[[TAGBL|PREC}} = Normal ; ENCUT = 250.0
ALGO = BSE 
ANTIRES = 0
ISMEAR = 0 ; SIGMA = 0.01
ENCUTGW = 150
EDIFF = 1.E-8
NBANDS = 128
NBANDSO = 4
NBANDSV = 8
OMEGAMAX = 20
PRECFOCK = Normal

By specifying ANTIRES=0 we use the Tamm-Dancoff approximation.
ENCUTGW=150 specifies the energy cut-off of the response function.
NBANDSO and NBANDSV define the number of valence and conduction bands in the calculations.
This calculation needs the orbitals (WAVECAR file) from step 3 and the derivative of the orbitals with respect to the Bloch vectors (WAVEDER file) written in step 2.
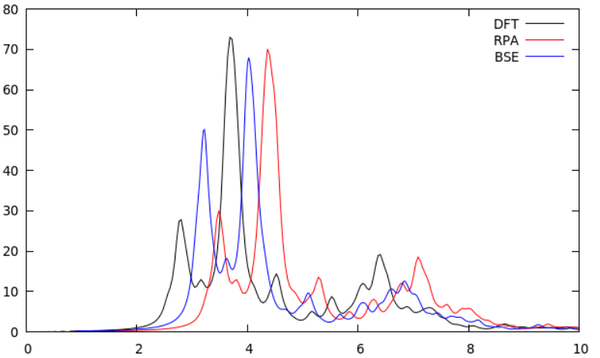
By using the script ./plotall.sh we get the absorption spectra within the independent particle picture and with BSE:

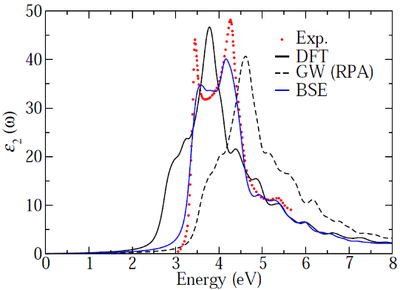
The calculated dielectric function of Si is at this point (GW+BSE) already in much better agreement with experiment. However we can do even better as shown in the following figure:

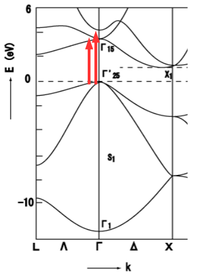
The problem comes from the coarse k-point grid that we have used. A denser grid samples more (direct) transitions between the bands.

Simply using a denser grid is mostly not an option because of the computational expense.

Used INCAR Tags

ALGO, ANTIRES, EDIFF, ENCUT, ENCUTGW, IALGO, IMIX, ISMEAR, KPAR, LOPTICS, LPEAD, LWAVE, NBANDS, NBANDSGW, NBANDSO, NBANDSV, NELM, NKRED, NOMEGA, OMEGAMAX, OMEGATL, PREC, PRECFOCK, SIGMA

Download

Si_BSE.tgz

Overview > Dielectric properties of Si using BSE > Improving the dielectric function > Plotting the BSE fatband structure of Si > List of tutorials

Back to the main page

@@ Line 120: / Line 120: @@
 [[File:Fig BSE example1 2.png|600px]]
 *The calculated dielectric function of Si is at this point (GW+BSE) already in much better agreement with experiment. However we can do even better as shown in the following figure:
-[[File:Fig BSE example1 4.png|600px]]
+[[File:Fig BSE example1 4.png|400px]]
 *The problem comes from the coarse k-point grid that we have used. A denser grid samples more (direct) transitions between the bands.
-[[File:Fig BSE example1 3.png|400px]]
+[[File:Fig BSE example1 3.png|200px]]
 *Simply using a denser grid is mostly not an option because of the computational expense.