O dimer

Overview > O atom > O atom spinpolarized > O atom spinpolarized low symmetry > O dimer > CO > CO vibration > CO partial DOS > H2O > H2O vibration > H2O molecular dynamics > Further things to try  > List of tutorials

Task

Relaxation of the bond length of an oxygen dimer.

Input

POSCAR

O dimer in a box
 1.0          ! universal scaling parameters
 8.0 0.0 0.0  ! lattice vector  a(1)
 0.0 8.0 0.0  ! lattice vector  a(2)
 0.0 0.0 8.0  ! lattice vector  a(3)
2             ! number of atoms
cart          ! positions in cartesian coordinates
 0 0 0        ! first atom
 0 0 1.22     ! second atom

INCAR

SYSTEM = O2 dimer in a box
ISMEAR = 0 ! Gaussian smearing
ISPIN  = 2 ! spin polarized calculation
NSW = 5    ! 5 ionic steps
IBRION = 2 ! use the conjugate gradient algorithm

KPOINTS

Gamma-point only
 0
Monkhorst Pack
 1 1 1
 0 0 0

Calculation

• We have selected in the INCAR file that geometry relaxation should be performed. In this case 5 ionic steps (NSW=5) should be done at most. For the relaxation a conjugate gradient (CG) algorithm is used (IBRION=2).

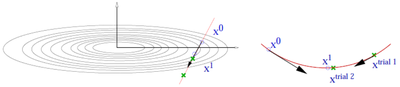
• The CG algorithm requires line minimizations along the search direction. This is done using a variant of Brent's algorithm. (Picture missing)
  • Trial step along search direction (gradient scaled by POTIM)
  • Quadratic or cubic interpolation using energies and forces at $\mathbf{x}_{0}$ and $\mathbf{x}_{1}$ allows to determine the approximate minimum
  • Continue minimization, if app. minimum is not accurate enough

stdout

DAV:   1     0.517118590134E+02    0.51712E+02    -0.31393E+03    80   0.366E+02
...    ...   ...
...    ...   ...
DAV:  14    -0.985349953776E+01   -0.15177E-03    -0.57546E-06    64   0.125E-02    0.371E-03
DAV:  15    -0.985357023804E+01   -0.70700E-04    -0.22439E-06    64   0.741E-03
   1 F= -.98535702E+01 E0= -.98535702E+01  d E =-.985357E+01  mag=     2.0000
 curvature:   0.00 expect dE= 0.000E+00 dE for cont linesearch  0.000E+00
 trial: gam= 0.00000 g(F)=  0.113E+00 g(S)=  0.000E+00 ort = 0.000E+00 (trialstep = 0.100E+01)
 search vector abs. value=  0.113E+00
 bond charge predicted
...    ...   ...
...    ...   ...
   2 F= -.96234585E+01 E0= -.96234585E+01  d E =0.230112E+00  mag=      2.0000
 trial-energy change:    0.230112  1 .order    0.190722   -0.113406    0.494850
 step:   0.1397(harm=  0.1864)  dis= 0.00731  next Energy=    -9.861386 (dE=-0.782E-02)
 bond charge predicted
...    ...   ...
...    ...   ...
   3 F= -.98607735E+01 E0= -.98607735E+01  d E =-.720327E-02  mag=      2.0000
 curvature:  -0.09 expect dE=-0.900E-05 dE for cont linesearch -0.900E-05
 trial: gam= 0.00000 g(F)=  0.969E-04 g(S)=  0.000E+00 ort =-0.331E-02 (trialstep = 0.828E+00)
 search vector abs. value=  0.969E-04
 reached required accuracy - stopping structural energy minimisation

Explanation of the output:

• The quantitiy trial-energy change is the change of the energy in the trial step.

• The first value after 1. order is the expected energy change calculated from the forces $((\mathbf{F}(\textrm{start})+\mathbf{F}(\textrm{trial}))/2\times$ change of positions - central difference.

• The second and third value correspond to $\mathbf{F}(\mathrm{start}) \times$ change of positions and $\mathbf{F} (\mathrm{trial}) \times$ change of position.

• The value step is the estimated size of the step leading to a line minimization along the current search direction. harm is the optimal step using a second order (or harmonic) interpolation.

• The trial step sizde can be controlled by the paramter POTIM.

• The final positions after the optimization are stored in the CONTCAR file. One can copy CONTCAR to POSCAR and continue the relaxation.

Download

Odimer.tgz

---

To the list of examples or to the main page