Pulay stress

Pseudopotential calculations are calculate the energy of a cell using a finite number of plane waves and a finite number of k-points. When comparing between cells of different sizes, i.e.g volume, this results in them each having different plane wave basis sets. This would be solved by using an infinite number of k-points and plane waves. In practice, a large enough plane wave energy cutoff and number of k-points leads to converged energies. However, when the basis set is too small, i.e. prematurely truncated, this results in discontinuities in the total energy between cells of varying volumes. These discontinuities between energy and volume creates stress that decreases the volume compared to fully converged calculations, due to the diagonal components of the stress tensor being incorrect. This is the "Pulay stress". Figures 1 and 2 shows these discontinuities for diamond for prematurely truncated energy cutoffs and k-point meshes, respectively, in comparison to converged curves. It may be corrected for using a few different methods in VASP.

Fig 1. Total energy vs lattice parameter for converged and unconverged plane wave energy cutoffs. Diamond in a primitive cell. 2x2x2 k-point mesh.

Fig 2. Total energy vs lattice parameter for converged and unconverged k-point meshes. Diamond in a primitive cell. 250 eV energy cutoff.

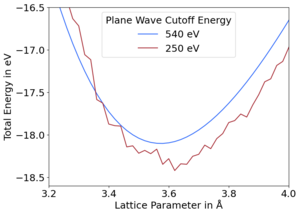
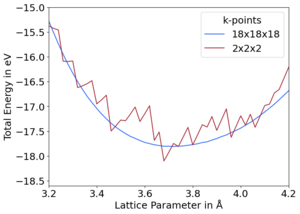
How to correct in VASP

The Pulay stress may be corrected in multiple ways. Generally, by calculating the relaxed structure with a larger basis-set by increasing the ENCUT:

1. Set ENCUT to $1.3\times$ the default cutoff, or PREC=High in VASP.4.4.
2. Re-run VASP with the default cutoff to obtain the final relaxed positions and cell parameters.

Accurate bulk relaxations with internal parameters (one)

If volume relaxations are necessary, follow this procedure:

Step 1.

Relax from the starting structure with Gaussian or Methfessel-Paxton smearing (ISMEAR = 0 or 1).

Step 2.

Copy the CONTCAR to POSCAR and relax the structure again.

Step 3.

Change the smearing method to the tetrahedron method (i.e. ISMEAR=-5) and perform a single point calculation, i.e. no relaxation of structure. These are will give highly accurate energies.

This should give good energies. If there are still problems, a few more additional steps can be tried.

Step 4a.

If there are still problems, try further increasing the ENCUT.

Step 4b.

If the default energy cutoff must be used for the relaxations, then an alternative procedure may be followed.

1. Perform a single point calculation for starting structure with a higher ENCUT. In the OUTCAR file, good estimation for the Pulay stress is given as a negative pressure, e.g.:
2. external pressure = -100.29567 kB
3. Add PSTRESS to the INCAR.
5. Set it equal to the Pulay stress given by the 'external pressure' in the OUTCAR.

6. Accurate bulk relaxations with internal parameters (two)

   It is possible to avoid volume relaxation in many cases:

   • Relax the structure (cell shape and internal parameters) for a set of fixed volumes (ISIF=4).
   • Fit to an equation of state , e.g. Murnaghan.

   The outline for such a calculation is almost the same as in the previous section. But in this case, one has to do the calculations for a set of fixed volumes. At first sight, this seems to be much more expensive than method number one (outlined in the previous section). But in many cases, the additional costs are only small, because the internal parameters do not change very much from volume to volume. The following steps have to be done in these calculations:

   • Select one volume and relax from starting structure keeping the volume fixed (ISIF=4; ISMEAR=0 or 1).
   • Start a second relaxation (structure or electronic relaxation?) from the previous CONTCAR file (if the initial cell shape was reasonable this step can be skipped if the cell shape is kept fixed, you never have run VASP twice).
   • As a final step, perform one more energy calculation with the tetrahedron method switched on (ISMEAR=-5), to get very accurate unambiguous energies (no relaxation for the final run).

   FAQ: Why is my energy vs. volume plot jagged

   This is a very common question from people who start to do calculations with plane wave codes. There are two reasons why the energy vs. volume plot looks jagged:

   • Basis set incompleteness. The basis set is discrete and incomplete, and when the volume changes, additional plane waves are added. That causes small discontinuous changes in the energy.
     • Solutions:
       • Use a larger plane wave cutoff: This is usually the preferred and simplest solution.
       • Use more k-points : this solves the problem, because the criterion for including a plane wave in the basis set is $\vert {\bf G} + {\bf k} \vert < {\bf G}_{\rm cut}$. This means at each k-point a different basis set is used, and additional plane waves are added at each k-point at different volumes. In turn, the energy vs. volume curve becomes smoother.
   • A second possible reason for the jagged E(V) curve is the use of PREC=Normal. For PREC=Accurate the FFT grids are chosen such that ${\bf H} \vert \phi>$ is exactly evaluated. For PREC=Normal the FFT grids are set to 3/4 of the value that is required for an exact evaluation of ${\bf H} \vert \phi>$. This introduces small errors because when the volume changes the FFT grids change discontinuously. In other words, at each volume a different FFT grid is used, causing the energy to jump discontinuously between different volumes.
     • Solutions:
       • Use PREC=Accurate, or increase the plane wave cutoff.
       • Set your FFT grids manually, and choose the one that is used per default for the largest volume (obviously a laborious solution).

   ---

   References