Plotting exciton wavefunction: Difference between revisions
No edit summary |
No edit summary |
||
| Line 1: | Line 1: | ||
Plotting the wavefunction of an exciton can be instrumental for analyzing the symmetry, position, and localization of the excitonic state. | |||
The exciton wavefunction | The exciton wavefunction <math>\psi_\lambda(r_e,r_h)=\sum_{vc} A_{vc}^\lambda \psi_v(r_h)\psi_c^*(r_e)</math> is written as a function of coordinates of two particles: one hole and one electron {{cite|gatti:prb:2013}}. In order to visualize this such function in 3D space we need to "fix" one of the coordinates: the position of the electron <math>\psi_\lambda(r^*_e,r_h)</math> or the position of the hole <math>\psi_\lambda(r_e,r^*_h)</math>. | ||
# How to fix the position of the particle: | |||
When fixing the position of the particle it is important to make sure that the hole or electron is not fixed exactly at the center of an atom as that can coincide with a node of the wavefunction and yield wrong results. Thus, make sure to shift the fixed coordinate slightly away from the center of the atom. Furthermore, the wavefunction of the fixed particle is taken at the nearest <math>\mathbf{G}</math>-vector, whose exact position is written in the {{FILE|OUTCAR}} file ('hole/electron position is fixed at:'). | |||
The position of the fixed particle is provided in direct (fractional) coordinates by tags {{TAG|BSEHOLE}} or {{TAG|BSEELECTRON}} for a hole or an electron, respectively. The tag {{TAG|NBSEEIG}} sets the number of excitons wavefunction that are computed. | |||
VASP can compute the charge density of a particular excitonic state, i.e., <math>\rho_\lambda(r)=\psi_\lambda(r^*_e,r_h)\psi^*_\lambda(r^*_e,r_h)</math> or <math>\rho_\lambda(r)=\psi_\lambda(r_e,r^*_h)\psi^*_\lambda(r_e,r^*_h)</math>, and writes the resulting charge density into {{FILE|CHGCAR}}.XX files, where XX stands for the index <math>\lambda</math> of the state. VASP computes the charge density by transforming the unit cell with k-points into a supercell. Thus, the exciton charge density is written for a supercell of dimensions <math>{\rm NKX}\times{\rm NKX}\times{\rm NKX}</math>. | |||
{{NB|warning| The size of CHGCAR.XX files can get very large. Estimate the CHGCAR.XX file size as follows: <math>(NGX*NKX)*(NGX*NKX)*(NGX*NKX)*18</math> bytes.}} | |||
The exciton charge density only accounts for the plane-wave part of the wave function, thus, all the augmentation terms are not | {{NB|warning|The exciton charge density only accounts for the plane-wave part of the wave function, thus, all the augmentation terms are not neglected.} | ||
The calculated excitonic states can be degenerate, i.e., multiple eigenvectors have the same energy, thus, it is important to add together all the degenerate states to be able to analyze the exction. | The calculated excitonic states can be degenerate, i.e., multiple eigenvectors have the same energy, thus, it is important to add together all the degenerate states to be able to analyze the exction. | ||
# Example: | # Example: | ||
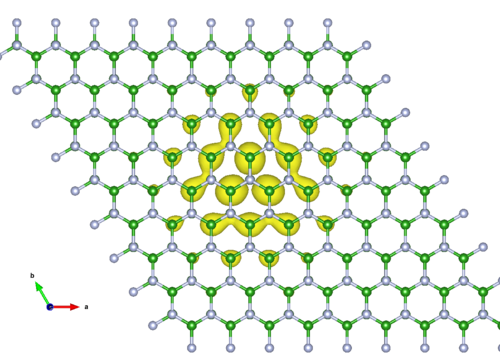
In the | In the figure, we provide an example, of the exciton wavefunction of the first bight excitonic state in hexagonal BN. | ||
Revision as of 15:54, 29 January 2024
Plotting the wavefunction of an exciton can be instrumental for analyzing the symmetry, position, and localization of the excitonic state.
The exciton wavefunction is written as a function of coordinates of two particles: one hole and one electron . In order to visualize this such function in 3D space we need to "fix" one of the coordinates: the position of the electron or the position of the hole .
- How to fix the position of the particle:
When fixing the position of the particle it is important to make sure that the hole or electron is not fixed exactly at the center of an atom as that can coincide with a node of the wavefunction and yield wrong results. Thus, make sure to shift the fixed coordinate slightly away from the center of the atom. Furthermore, the wavefunction of the fixed particle is taken at the nearest -vector, whose exact position is written in the OUTCAR file ('hole/electron position is fixed at:').
The position of the fixed particle is provided in direct (fractional) coordinates by tags BSEHOLE or BSEELECTRON for a hole or an electron, respectively. The tag NBSEEIG sets the number of excitons wavefunction that are computed.
VASP can compute the charge density of a particular excitonic state, i.e., or , and writes the resulting charge density into CHGCAR.XX files, where XX stands for the index of the state. VASP computes the charge density by transforming the unit cell with k-points into a supercell. Thus, the exciton charge density is written for a supercell of dimensions .
| Warning: The size of CHGCAR.XX files can get very large. Estimate the CHGCAR.XX file size as follows: bytes. |
{{NB|warning|The exciton charge density only accounts for the plane-wave part of the wave function, thus, all the augmentation terms are not neglected.}
The calculated excitonic states can be degenerate, i.e., multiple eigenvectors have the same energy, thus, it is important to add together all the degenerate states to be able to analyze the exction.
- Example:
In the figure, we provide an example, of the exciton wavefunction of the first bight excitonic state in hexagonal BN.
Related tags and sections
CHGCAR, NBSEEIG, BSEHOLE, BSEELECTRON, BSE
