Computing the work function

The work function is defined as the work needed to move an electron from a surface to a point in vacuum sufficiently far away from this surface. It is a central quantity in surface science, vacuum science, catalysis, and other related fields as it characterizes a given surface; illustrating the presence of impurities, adsorbates, and possible surface reconstruction. It is typically measured using surface science techniques such as thermionic emission, the Kelvin probe method, etc. It has also served as an important measure in various theoretical models about metallic surfaces. On this page, we describe how to compute the work function using outputs from a DFT calculation performed using VASP. We detail best practices, required INCAR tags, and possible pitfalls.

Mind: The work function is a property of a surface, not a bulk property. Hence, the content of this page only applies to systems with reduced dimensionality (such as surfaces), i.e., systems where there is expected to be a charge-density-free region in at least one direction of the cell.

Required quantities

The work function, ${\textstyle \Phi}$, is computed using the expression,

$$\Phi = e\phi_{\mathrm{vacuum}} - \varepsilon_{\mathrm{F}}$$

where ${\textstyle \phi_{\mathrm{vacuum}}}$ is the vacuum potential, i.e., the potential sufficiently far away from a surface, such that if an electron were to be placed at this position, it would not feel the presence of the surface. ${\textstyle \varepsilon_{F}}$ is the Fermi level of the surface, and ${\textstyle e}$ is the charge on the electron (equal to 1 in atomic units). In the next section, we describe how ${\textstyle \phi_{\mathrm{vacuum}}}$ and ${\textstyle \varepsilon_{F}}$ are determined from the LOCPOT and OUTCAR files, respectively.

Step-by-step instructions

Step 1: Ensure that the chosen structure has a large enough atom-free, i.e., charge-density-free, and field-free region in the direction normal to the surface. A good rule of thumb is to center the atoms in your cell and have anywhere between 8–12 Å of vacuum on either side in this direction.

Warning: An insufficiently large vacuum region causes a field within the vacuum region and, thus, leads to inaccurate values of the vacuum potential (see point 3).

Step 2: Perform a ground-state-DFT calculation. We suggest setting PREC=Accurate. If your cell has a net dipole moment, (i.e., it is not symmetric along the direction of the surface normal), we suggest switching on the dipole correction by using the following INCAR tags: LDIPOL, IDIPOL, DIPOL. The use of the dipole correction is crucial to obtaining a flat field-free region in the potential (c.f. next point). In addition to these tags, set the LVHAR=T to output only the Hartree and ionic potentials to the LOCPOT file.

Tip: We recommend using only the Hartree and ionic potentials as the exchange-correlation potential decays very slowly in vacuum. Using the sum of the Hartree and ionic potentials allows for determining the work function with significantly less vacuum requirements (and hence lower computational cost).

Step 3: Compute the vacuum potential. Average the contents of the LOCPOT file along the lattice vectors of the surface, (i.e., both directions perpendicular to the surface normal). Find the field-free region by determining the region of space where the potential remains constant. This value of the potential is the vacuum potential.

Tip: There exist two vacuum potential regions, one for either direction of the surface normal. Depending on your system, one of the directions may be more relevant than another.

Step 4: Determine the Fermi energy. The Fermi energy is written directly to the OUTCAR file. grep for the following lines in the OUTCAR to get the Fermi energy in eV.

  grep "Fermi energy" OUTCAR

Example

Vacuum potential referenced to the Fermi energy plotted against the distance along the surface normal. Insets to the figure show the work function for (red) a clean Pt(111) surface (blue) Pt(111) with a carbon atom adsorbed on only one surface termination (atom center ~15 Å on the x axis).

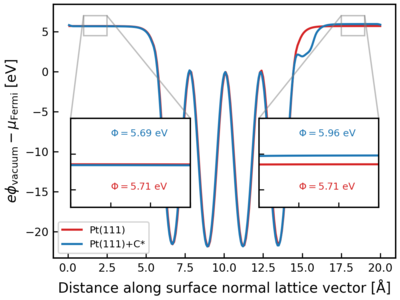
Consider an example of a carbon atom adsorbed on an fcc-Pt(111) surface. The structure of such a system is

Pt16C
1.0000000000000000
   5.5437171645025325    0.0000000000000000    0.0000000000000000
   0.0000000000000000    4.8009998958550284    0.0000000000000000
   0.0000000000000000    0.0000000000000000   20.0000000000000000
Pt C
16 1
Direct
   0.1250000000000000    0.0833333333333334    0.3302590208582500
   0.6250000000000000    0.0833333333333334    0.3302590208582500
   0.3749999999999999    0.5833333333333334    0.3302590208582500
   0.8750000000000001    0.5833333333333334    0.3302590208582500
   0.3749999999999999    0.2500000000000000    0.4434196736194167
   0.8750000000000001    0.2500000000000000    0.4434196736194167
   0.1250000000000000    0.7500000000000000    0.4434196736194167
   0.6250000000000000    0.7500000000000000    0.4434196736194167
   0.1250000000000000    0.4166666666666667    0.5565803263805833
   0.6250000000000000    0.4166666666666667    0.5565803263805833
   0.3749999999999999    0.9166666666666666    0.5565803263805833
   0.8750000000000001    0.9166666666666666    0.5565803263805833
   0.1250000000000000    0.0833333333333334    0.6697409791417500
   0.6250000000000000    0.0833333333333334    0.6697409791417500
   0.3749999999999999    0.5833333333333334    0.6697409791417500
   0.8750000000000001    0.5833333333333334    0.6697409791417500
   0.0000000000000000    0.0000000000000000    0.7597409791417501

The bottom and top surfaces are not identical: one is clean, and the other has carbon adsorbed on it. Since the system has a net dipole moment, we need to use the dipole correction in our calculation. An example INCAR file for this system is,

LDIPOL  = T
IDIPOL  = 3
DIPOL   = 0.5 0.5 0.5
LVHAR   = T
PREC    = Accurate

The Figure to the right shows a representative example of the vacuum potential obtained by averaging the contents of LOCPOT. This potential is referenced to the Fermi energy and is plotted against the distance along the surface normal (x axis) for two systems, fcc Pt(111) surface (in blue) and Pt(111) surface with a carbon atom adsorbed on one surface termination (Pt(111)-C*). The vacuum potentials are flat, (i.e., constant), on either side (magnified in insets). The work function on either side of the slab is annotated in the insets as ${\textstyle \Phi}$. It is equal for both sides of the clean slab, but slightly higher for the case of Pt(111)-C*.

Related tags and articles

LOCPOT, LDIPOL, IDIPOL, DIPOL