Biased molecular dynamics: Difference between revisions

Revision as of 09:16, 7 April 2023

The probability density for a geometric parameter ξ of the system driven by a Hamiltonian:

{\displaystyle H(q,p) = T(p) + V(q), \; }

with T(p), and V(q) being kinetic, and potential energies, respectively, can be written as:

{\displaystyle P(\xi_i)=\frac{\int\delta\Big(\xi(q)-\xi_i\Big) \exp\left\{-H(q,p)/k_B\,T\right\} dq\,dp}{\int \exp\left\{-H(q,p)/k_B\,T\right\}dq\,dp} = \langle\delta\Big(\xi(q)-\xi_i\Big)\rangle_{H}. }

The term $\langle X \rangle_H$ stands for a thermal average of quantity X evaluated for the system driven by the Hamiltonian H.

If the system is modified by adding a bias potential $\tilde{V}(\xi)$ acting on one or multiple selected internal coordinates of the system ξ=ξ(q), the Hamiltonian takes a form:

{\displaystyle \tilde{H}(q,p) = H(q,p) + \tilde{V}(\xi), }

and the probability density of ξ in the biased ensemble is:

{\displaystyle \tilde{P}(\xi_i)= \frac{\int \delta\Big(\xi(q)-\xi_i\Big) \exp\left\{-\tilde{H}(q,p)/k_B\,T\right\} dq\,dp}{\int \exp\left\{-\tilde{H}(q,p)/k_B\,T\right\}dq\,dp} = \langle\delta\Big(\xi(q)-\xi_i\Big)\rangle_{\tilde{H}} }

It can be shown that the biased and unbiased averages are related via a simple formula:

{\displaystyle P(\xi_i)=\tilde{P}(\xi_i) \frac{\exp\left\{\tilde{V}(\xi)/k_B\,T\right\}}{\langle \exp\left\{\tilde{V}(\xi)/k_B\,T\right\} \rangle_{\tilde{H}}}. }

More generally, an observable $\langle A \rangle_{H}$ :

{\displaystyle \langle A \rangle_{H} = \frac{\int A(q) \exp\left\{-H(q,p)/k_B\,T\right\} dq\,dp}{\int \exp\left\{-H(q,p)/k_B\,T\right\}dq\,dp} }

can be expressed in terms of thermal averages within the biased ensemble:

{\displaystyle \langle A \rangle_{H} =\frac{\langle A(q) \,\exp\left\{\tilde{V}(\xi)/k_B\,T\right\} \rangle_{\tilde{H}}}{\langle \exp\left\{\tilde{V}(\xi)/k_B\,T\right\} \rangle_{\tilde{H}}}. }

Simulation methods such as umbrella sampling^[1] use a bias potential to enhance sampling of ξ in regions with low P(ξ_i) such as transition regions of chemical reactions. The correct distributions are recovered afterwards using the equation for $\langle A \rangle_{H}$ above.

A more detailed description of the method can be found in Ref.^[2]. Biased molecular dynamics can be used also to introduce soft geometric constraints in which the controlled geometric parameter is not strictly constant, instead it oscillates in a narrow interval of values. The bias potentials are supported in both the NVT and NpT MD simulations regardless of the particular thermostat and/or barostat setting. Different types of potentials can be freely combined.

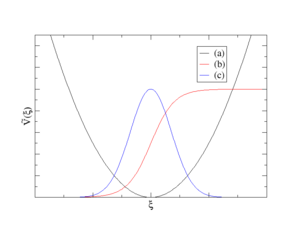
Supported types of bias potentials

Presently, the following types of bias potential are supported:

sum of Harmonic potentials (see curve (a) on the plot above)

{\displaystyle \tilde{V}(\xi_1,\dots,\xi_{M_8}) = \sum_{\mu=1}^{M}\frac{1}{2}\kappa_{\mu} (\xi_{\mu}(q)-\xi_{0\mu})^2 \; }

where the sum runs all ( $M_8$ ) coordinates the potential acts upon, which are defined in the ICONST-file by setting the status to 8. The parameters of the potential, $\kappa_{\mu}$ (force constant) and $\xi_{0\mu}$ (minimum of potential), are defined, respectively, via the keywords SPRING_K and SPRING_R0 in INCAR. Optionally, it is also possible to change the value of $\xi_{0\mu}$ every MD step at a constant rate defined via parameter SPRING_V. The number of items defined via SPRING_K, SPRING_R0, and SPRING_V must be equal to $M_8$ , otherwise the calculation terminates with an error message. This form of bias potential is employed in several simulation protocols, such as the umbrella sampling^[1], umbrella integration, or steered MD, and is useful also in cases where the $\xi_{\mu}$ values need restrained.

sum of Fermi-like step functions (see curve (b) on the plot above)

{\displaystyle \tilde{V}(\xi_1,\dots,\xi_{M_4}) = \sum_{\mu=1}^{M_4}\frac{A_{\mu}}{1+\text{exp}\left [-D_{\mu}(\frac{\xi(q)}{\xi_{0\mu}} -1) \right ]} \; }

where the sum runs all ( $M_4$ ) coordinates the potential acts upon, which are defined in the ICONST-file by setting the status to 4. The parameters of the potential, $A_{\mu}$ (the height of step), $D_{\mu}$ (controlling the slope around the point $\xi_{0\mu}$ ), and $\xi_{0\mu}$ (position of the step), are defined, respectively, via the keywords FBIAS_A, FBIAS_D, and FBIAS_R0 in INCAR. The number of items defined via FBIAS_A, FBIAS_D, and FBIAS_R0 must be equal to $M_4$ , otherwise the calculation terminates with an error message. This form of potential is suitable especially for imposing restriction on the upper (or lower) limit of value of $\xi$ .

sum of Gauss functions (see curve (b) on the plot above)

{\displaystyle \tilde{V}(\xi_1,\dots,\xi_{M}) = \sum_{\nu=1}^{N_5}h_{\nu}\text{exp}\left [-\frac{\sum_{\mu=1}^{M_5}(\xi_{\mu}(q)-\xi_{0\nu,\mu})^2}{2w_{\nu}^2} \right ], \; }

where $N_5$ is the number of Gaussian functions and $M_5$ is the number of coordinates the potential acts upon. The latter defined in the ICONST-file by setting the status to 5. The parameters of the potentials, $h_{\nu}$ , $w_{\nu}$ , and $\xi_{0\nu,\mu}$ are defined in the PENALTYPOT-file. The this type of bias potential is primarily intended for the use in metadynamics but since Gaussians can be used as basis functions for more general shapes, they can be used also to prepare various atypically-shaped bias potentials.

Examples of usage

As a concrete example, let us consider the nucleophile substitution reaction of CH $_3$ Cl with Cl $^-$ . The reactant is a weak vdW complex shown on the figure below, the corresponding POSCAR-file is

vdW complex CH3Cl...Cl 
1.00000000000000
12.0000000000000000    0.0000000000000000    0.0000000000000000
0.0000000000000000    12.0000000000000000    0.0000000000000000
0.0000000000000000    0.0000000000000000    12.0000000000000000
C H Cl
1 3 2
cart
5.91331371  7.11364924  5.78037960
5.81982231  8.15982106  5.46969017
4.92222130  6.65954232  5.88978969
6.47810398  7.03808479  6.71586385
4.32824726  8.75151396  7.80743202
6.84157897  6.18713289  4.46842049

due to weak interactions between CH $_3$ Cl and Cl $^-$ , the complex can collapse at high temperature. This can be avoided by setting an upper bound for the length of the non-bonding Cl...C interactions, which can can conveniently be achieved by using a Fermi-shaped bias potential. To this end, we need to define the Cl...C distance (distance between the atoms 1 and 5) as a coordinate with status 4 in the ICONST-file:

R 1 5 4

Next, we need to specify the bias potential parameters FBIAS_A, FBIAS_D, and FBIAS_R0 in the ICONST-file. Since the bias potential acts only on one internal coordinate, we need to provide only one single number for each of these flags. As shown in Fig.3, the setting

FBIAS_A  = 1
FBIAS_D  = 50
FBIAS_R0 = 3.5

ensures that repulsive bias forces steeply increase when the C...Cl distance is increased beyond about 3.2 A, which would in effect cause shortening of the distance in next MD step. Notice that the bias force is essentially negligible for distances below 3 A. A careful adjustment of $A$ and $D$ is needed to ensure that (i) the bias force is large enough to effectively limit the value of $\xi$ , and (ii) the interval of $\xi$ values for which the bias forces are significant is broad enough to avoid its overcoming via random fluctuations. A suitable setting can be found by inspecting the analytical expression for the potential from which it is obvious that the maximal bias force of $\frac{D\,A}{4\xi_0}$ is exerted on the system at the point $\xi = \xi_{0}$ .

Andersen thermostat

For a biased molecular dynamics run with Andersen thermostat, one has to:

Set the standard MD-related tags: IBRION=0, TEBEG, POTIM, and NSW
Set MDALGO=1 (MDALGO=11 in VASP 5.x), and choose an appropriate setting for ANDERSEN_PROB
In order to avoid updating of the bias potential, set HILLS_BIN=NSW
Define collective variables in the ICONST-file, and set the STATUS parameter for the collective variables to 5
Define the bias potential in the PENALTYPOT-file

Nose-Hoover thermostat

For a biased molecular dynamics run with Nose-Hoover thermostat, one has to:

Set the standard MD-related tags: IBRION=0, TEBEG, POTIM, and NSW
Set MDALGO=2 (MDALGO=21 in VASP 5.x), and choose an appropriate setting for SMASS
In order to avoid updating of the bias potential, set HILLS_BIN=NSW
Define collective variables in the ICONST-file, and set the STATUS parameter for the collective variables to 5
Define the bias potential in the PENALTYPOT-file

The values of all collective variables for each MD step are listed in the REPORT-file, check the lines after the string Metadynamics.

References

↑ ^a ^b G. M. Torrie and J. P. Valleau, J. Comp. Phys. 23, 187 (1977).
↑ D. Frenkel and B. Smit, Understanding molecular simulations: from algorithms to applications, Academic Press: San Diego, 2002.

[Torrie77-1] G. M. Torrie and J. P. Valleau, J. Comp. Phys. 23, 187 (1977).

[FrenkelSmit-2] D. Frenkel and B. Smit, Understanding molecular simulations: from algorithms to applications, Academic Press: San Diego, 2002.

[1]

[2]

@@ Line 58: / Line 58: @@
 *sum of Fermi-like step functions (see curve (b) on the plot above)
 :<math>
-\tilde{V}(\xi_1,\dots,\xi_{M_4}) = \sum_{\mu=1}^{M_4}\frac{A_{\mu}}{1+\text{exp}\left [-D_{\mu}\frac{\xi(q)}{\xi_{0\mu}} -1 \right ]} \;
+\tilde{V}(\xi_1,\dots,\xi_{M_4}) = \sum_{\mu=1}^{M_4}\frac{A_{\mu}}{1+\text{exp}\left [-D_{\mu}(\frac{\xi(q)}{\xi_{0\mu}} -1) \right ]} \;
 </math>
 where the sum runs all (<math>M_4</math>) coordinates the potential acts upon, which are defined in the {{FILE|ICONST}}-file by setting the status to 4.
@@ Line 93: / Line 93: @@
 .32824726  8.75151396  7.80743202
 .84157897  6.18713289  4.46842049
+* due to weak interactions between CH<math>_3</math>Cl and Cl<math>^-</math>, the complex  can collapse at high temperature. This can be avoided by setting an upper bound for the length of the non-bonding Cl...C interactions, which can can conveniently be achieved by using a Fermi-shaped bias potential. To this end, we need to define the Cl...C distance (distance between the atoms 1 and 5) as a coordinate with status 4 in the {{FILE|ICONST}}-file:
+ R 1 5 4
+Next, we need to specify the bias potential parameters {{TAG|FBIAS_A}}, {{TAG|FBIAS_D}}, and {{TAG|FBIAS_R0}} in the {{FILE|ICONST}}-file. Since the bias potential acts only on one internal coordinate, we need to provide only one single number for each of these flags. As shown in Fig.3, the setting
+ FBIAS_A  = 1
+ FBIAS_D  = 50
+ FBIAS_R0 = 3.5
+ensures that repulsive bias forces steeply increase when the C...Cl distance is increased beyond about 3.2 A, which would in effect cause shortening of the distance in next MD step. Notice that the bias force is essentially negligible for distances below 3 A.
+A careful adjustment of <math>A</math> and <math>D</math> is needed to ensure that (i) the bias force is large enough to effectively limit the value of <math>\xi</math>, and (ii) the interval of  <math>\xi</math> values for which the bias forces are significant is broad enough to avoid its overcoming via random fluctuations.
+A suitable setting can be found by inspecting the  analytical expression for the potential from which it is obvious that the maximal bias force of <math>\frac{D\,A}{4\xi_0}</math> is exerted on the system at the point <math>\xi = \xi_{0}</math>.
 == Andersen thermostat ==
@@ Line 101: / Line 115: @@
 #In order to avoid updating of the bias potential, set {{TAG|HILLS_BIN}}={{TAG|NSW}}
 #Define collective variables in the {{FILE|ICONST}}-file, and set the <tt>STATUS</tt> parameter for the collective variables to 5
 #Define the bias potential in the {{FILE|PENALTYPOT}}-file
 == Nose-Hoover thermostat ==