Equilibrium volume of Si in the RPA: Difference between revisions
Vaspmaster (talk | contribs) |
|||
| (29 intermediate revisions by 2 users not shown) | |||
| Line 3: | Line 3: | ||
== Task == | == Task == | ||
In this example you will calculate the equilibrium lattice constant of Si in the RPA (ACFDT). | |||
The workflow of a RPA total energy calculations consists of five consecutive steps: | |||
# a “standard” DFT groundstate calculation with a “dense” mesh of k-points. | |||
# compute the Hartree-Fock energy using the DFT orbitals of Step 1. Needs {{TAG|WAVECAR}} file from step 1. | |||
# a “standard” DFT groundstate calculation with “coarse” mesh of k-points. | |||
# obtain DFT “virtual” orbitals (empty states). Needs {{TAG|WAVECAR}} file from step 3. | |||
# the RPA correlation energy (ACFDT) calculation. Needs {{TAG|WAVECAR}} and {{TAG|WAVEDER}} files from step 4. | |||
In case of metallic systems there is an additional step between Steps 4 and 5, that is beyond the | |||
scope of this example. | |||
'''N.B.:'''To compute the equilibrium lattice constant of Si we need to calculate the RPA total energy for a range of different lattice constants. | |||
All of the calculation steps are prepared automatically performed by the script ''doall.sh'' (see below): | |||
./doall.sh | |||
This script will perform the following calculations for a range of different lattice constants: | |||
=== Step 1: DFT groundstate calculation with a “dense” mesh of k-points === | === Step 1: DFT groundstate calculation with a “dense” mesh of k-points === | ||
| Line 44: | Line 35: | ||
12 12 12 | 12 12 12 | ||
0 0 0 | 0 0 0 | ||
=== Step 2: Compute the Hartree-Fock energy using the DFT orbitals=== | === Step 2: Compute the Hartree-Fock energy using the DFT orbitals=== | ||
| Line 50: | Line 42: | ||
*The {{TAG|INCAR}} file INCAR.EXX is used in this step: | *The {{TAG|INCAR}} file INCAR.EXX is used in this step: | ||
{{TAGBL|ALGO}} = EIGENVAL ; {{TAGBL|NELM}} = 1 | {{TAGBL|ALGO}} = EIGENVAL ; {{TAGBL|NELM}} = 1 | ||
{{TAGBL|LWAVE}} = .FALSE. | {{TAGBL|LWAVE}} = .FALSE. | ||
| Line 60: | Line 53: | ||
*{{TAG|NKRED}}=2 is used for the downsample the k-space representation of the Fock-potential to save time. | *{{TAG|NKRED}}=2 is used for the downsample the k-space representation of the Fock-potential to save time. | ||
*Using {{TAG|NBANDS}}=4 only occupied states are considered to save time. | *Using {{TAG|NBANDS}}=4 only occupied states are considered to save time. | ||
=== Step 3 === | |||
*DFT groundstate calculation with a “coarse” mesh of k-points. | === Step 3: DFT groundstate calculation with a “coarse” mesh of k-points === | ||
*Perform a DFT groundstate calculation with a “coarse” mesh of k-points. | |||
:This is the mesh of k-points that will be used in the subsequent ACFDT calculation. | |||
*The following {{TAG|INCAR}} file is used (INCAR.DFT): | *The following {{TAG|INCAR}} file is used (INCAR.DFT): | ||
{{TAGBL|ISMEAR}} = 0 ; {{TAGBL|SIGMA}} = 0.05 | {{TAGBL|ISMEAR}} = 0 ; {{TAGBL|SIGMA}} = 0.05 | ||
{{TAGBL|EDIFF}} = 1E-8 | {{TAGBL|EDIFF}} = 1E-8 | ||
*The following coarse {{TAG|KPOINTS}} file is used (KPOINTS. | |||
*The following coarse {{TAG|KPOINTS}} file is used (KPOINTS.6): | |||
6x6x6 | 6x6x6 | ||
0 | 0 | ||
| Line 74: | Line 73: | ||
0 0 0 | 0 0 0 | ||
=== Step 4 === | |||
=== Step 4: Obtain DFT "virtual" orbitals (empty states) === | |||
*Obtain DFT "virtual" orbitals (empty states). | *Obtain DFT "virtual" orbitals (empty states). | ||
*The following {{TAG|INCAR}} file is used in this step (INCAR.DIAG): | *The following {{TAG|INCAR}} file is used in this step (INCAR.DIAG): | ||
{{TAGBL|ALGO}} = Exact | {{TAGBL|ALGO}} = Exact | ||
| Line 82: | Line 84: | ||
{{TAGBL|LOPTICS}} = .TRUE. | {{TAGBL|LOPTICS}} = .TRUE. | ||
{{TAGBL|ISMEAR}} = 0 ; {{TAGBL|SIGMA}} = 0.05 | {{TAGBL|ISMEAR}} = 0 ; {{TAGBL|SIGMA}} = 0.05 | ||
*In this step one needs to set {{TAG|LOPTICS}}=''.TRUE.'' | |||
*In this step one needs to set {{TAG|LOPTICS}}=''.TRUE.'' so that VASP calculates the derivative of the orbitals w.r.t. the Bloch wavevector (stored in the {{TAG|WAVEDER}} file). These are needed to correctly describe the long-wavelength limit of the dielectric screening. | |||
*We use exact diagonalization ({{TAG|ALGO}}=''Exact'') and keep 64 bands after diagonalization ({{TAG|NBANDS}}=64). | *We use exact diagonalization ({{TAG|ALGO}}=''Exact'') and keep 64 bands after diagonalization ({{TAG|NBANDS}}=64). | ||
*This calculations needs the orbitals ({{TAG|WAVECAR}} file) written in Step 3. | *This calculations needs the orbitals ({{TAG|WAVECAR}} file) written in Step 3. | ||
=== Step 5 | |||
=== Step 5: calculate the RPA correlation energy (ACFDT) === | |||
*The following {{TAG|INCAR}} file is used in this step (INCAR.ACFDT): | *The following {{TAG|INCAR}} file is used in this step (INCAR.ACFDT): | ||
{{TAGBL|ALGO}} = ACFDT | {{TAGBL|ALGO}} = ACFDT | ||
{{TAGBL|NBANDS}} = 64 | {{TAGBL|NBANDS}} = 64 | ||
{{TAGBL|ISMEAR}} = 0 ; {{TAGBL|SIGMA}} = 0.05 | {{TAGBL|ISMEAR}} = 0 ; {{TAGBL|SIGMA}} = 0.05 | ||
*In OUTCAR.ACFDT.X.X one finds the RPA correlation energy, e.g.: | *In OUTCAR.ACFDT.X.X one finds the RPA correlation energy, e.g.: | ||
<pre> | |||
cutoff energy smooth cutoff RPA correlation Hartree contr. to MP2 | cutoff energy smooth cutoff RPA correlation Hartree contr. to MP2 | ||
--------------------------------------------------------------------------------- | --------------------------------------------------------------------------------- | ||
| Line 105: | Line 111: | ||
linear regression | linear regression | ||
converged value -10.9079580568 -19.1711146204 | converged value -10.9079580568 -19.1711146204 | ||
</pre> | |||
*Take the “converged value”, in this case: ''EC(RPA) = -10.9079580568''eV (an approximate “infinite basis set” limit). | *Take the “converged value”, in this case: ''EC(RPA) = -10.9079580568''eV (an approximate “infinite basis set” limit). | ||
*This calculations needs the orbitals ({{TAG|WAVECAR}} file) and the derivative of the orbitals w.r.t. the Bloch wavevectors ({{TAG|WAVEDER}} file) written in Step 4. | *This calculations needs the orbitals ({{TAG|WAVECAR}} file) and the derivative of the orbitals w.r.t. the Bloch wavevectors ({{TAG|WAVEDER}} file) written in Step 4. | ||
*The RPA total energy is calculated as the, ''E(RPA)=EC(RPA)+EXX'' sum of the RPA correlation energy of step 5 ''EC(RPA)'' and the Hartree fock energy ''EXX''. To get the Hartree fock energy grep “free energy” in the OUTCAR.EXX.* file (there are two spaces between free and energy). | |||
*The RPA total energy is calculated as the, ''E(RPA)=EC(RPA)+EXX'', the sum of the RPA correlation energy of step 5 ''EC(RPA)'' and the Hartree fock energy ''EXX'' of step 2. | |||
:To get the Hartree fock energy <code>grep “free energy”</code> in the OUTCAR.EXX.* file (there are two spaces between free and energy). | |||
== Running this example == | |||
The following bash-script <code>doall.sh</code> will run through all of the aforementioned calculational steps (step 1-5) for a range of different lattice constants (''a=5.1-5.8'' Å in steps of ''0.1'' Å) | |||
<pre> | |||
# | |||
# To run VASP this script calls $vasp_std | |||
# (or posibly $vasp_gam and/or $vasp_ncl). | |||
# These variables can be defined by sourcing vaspcmd | |||
. vaspcmd 2> /dev/null | |||
# | |||
# When vaspcmd is not available and $vasp_std, | |||
# $vasp_gam, and/or $vasp_ncl are not set as environment | |||
# variables, you can specify them here | |||
[ -z "`echo $vasp_std`" ] && vasp_std="mpirun -np 8 /path-to-your-vasp/vasp_std" | |||
[ -z "`echo $vasp_gam`" ] && vasp_gam="mpirun -np 8 /path-to-your-vasp/vasp_gam" | |||
[ -z "`echo $vasp_ncl`" ] && vasp_ncl="mpirun -np 8 /path-to-your-vasp/vasp_ncl" | |||
# | |||
# The real work starts here | |||
# | |||
for i in 5.1 5.2 5.3 5.4 5.5 5.6 5.7 5.8 ; do | |||
cat >POSCAR <<! | |||
system Si | |||
$i | |||
0.5 0.5 0.0 | |||
0.0 0.5 0.5 | |||
0.5 0.0 0.5 | |||
2 | |||
cart | |||
0.00 0.00 0.00 | |||
0.25 0.25 0.25 | |||
! | |||
# start with a PBE calculation with a lot of k-points (needed for EXX) | |||
rm WAVECAR WAVEDER | |||
cp KPOINTS.12 KPOINTS | |||
cp INCAR.DFT INCAR | |||
$vasp_std | |||
cp OUTCAR OUTCAR.DFT.$i | |||
e1=`awk '/free energy/ {print $5}' OUTCAR` | |||
# get the HF energy with PBE orbitals | |||
cp INCAR.EXX INCAR | |||
$vasp_std | |||
e2=`awk '/free energy/ {print $5}' OUTCAR` | |||
cp OUTCAR OUTCAR.EXX.$i | |||
# now a PBE calculation with less k-points | |||
rm WAVECAR WAVEDER | |||
cp KPOINTS.6 KPOINTS | |||
cp INCAR.DFT INCAR | |||
$vasp_std | |||
# obtain virtual orbitals | |||
cp INCAR.DIAG INCAR | |||
$vasp_std | |||
cp OUTCAR OUTCAR.DIAG.$i | |||
cp WAVECAR WAVECAR.$i | |||
cp WAVEDER WAVEDER.$i | |||
## for metals | |||
# cp INCAR.HFC INCAR | |||
# $vasp_std | |||
# | |||
# cp OUTCAR OUTCAR.HFC.$i | |||
# e3=`awk '/HF-correction/ {print $4}' OUTCAR` | |||
# RPA correlation | |||
cp INCAR.ACFDT INCAR | |||
$vasp_std | |||
cp OUTCAR OUTCAR.ACFDT.$i | |||
e4=`awk '/converged value/ {print $3}' OUTCAR` | |||
# echo $i $e1 $e2 $e3 $e4 >> summary | |||
echo $i $e1 $e2 $e4 >> summary | |||
done | |||
</pre> | |||
To execute the aforementions script: | |||
./doall.sh | |||
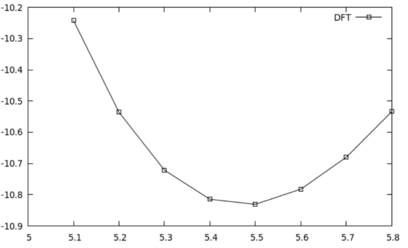
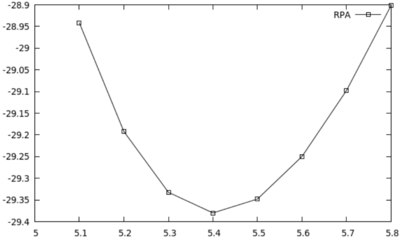
* When everything is finished you can quickly visualize (with gnuplot) the total energy vs. lattice-constant curves for DFT and RPA by means of: | |||
./plotall.sh | |||
[[File:Fig ACFDT 1 a.png|408px]] | [[File:Fig ACFDT 1 a.png|408px]] | ||
| Line 117: | Line 224: | ||
== Download == | == Download == | ||
[ | [[Media:Si ACFDT vol.tgz| Si_ACFDT_vol.tgz]] | ||
{{Template:GW - Tutorial}} | {{Template:GW - Tutorial}} | ||
[[Category:Examples]] | [[Category:Examples]] | ||
Latest revision as of 13:21, 14 November 2019
Task
In this example you will calculate the equilibrium lattice constant of Si in the RPA (ACFDT).
The workflow of a RPA total energy calculations consists of five consecutive steps:
- a “standard” DFT groundstate calculation with a “dense” mesh of k-points.
- compute the Hartree-Fock energy using the DFT orbitals of Step 1. Needs WAVECAR file from step 1.
- a “standard” DFT groundstate calculation with “coarse” mesh of k-points.
- obtain DFT “virtual” orbitals (empty states). Needs WAVECAR file from step 3.
- the RPA correlation energy (ACFDT) calculation. Needs WAVECAR and WAVEDER files from step 4.
In case of metallic systems there is an additional step between Steps 4 and 5, that is beyond the scope of this example.
N.B.:To compute the equilibrium lattice constant of Si we need to calculate the RPA total energy for a range of different lattice constants. All of the calculation steps are prepared automatically performed by the script doall.sh (see below):
./doall.sh
This script will perform the following calculations for a range of different lattice constants:
Step 1: DFT groundstate calculation with a “dense” mesh of k-points
- The following INCAR file is used (INCAR.DFT):
ISMEAR = 0 ; SIGMA = 0.05 EDIFF = 1E-8
- The following KPOINTS file is used (KPOINTS.12):
12x12x12 0 G 12 12 12 0 0 0
Step 2: Compute the Hartree-Fock energy using the DFT orbitals
- To Compute the Hartree-Fock energy using DFT orbitals we need the (WAVECAR) of Step 1.
- The INCAR file INCAR.EXX is used in this step:
ALGO = EIGENVAL ; NELM = 1 LWAVE = .FALSE. LHFCALC = .TRUE. AEXX = 1.0 ; ALDAC = 0.0 ; AGGAC = 0.0 NKRED = 2 ISMEAR = 0 ; SIGMA = 0.05 KPAR = 8 NBANDS = 4
- NKRED=2 is used for the downsample the k-space representation of the Fock-potential to save time.
- Using NBANDS=4 only occupied states are considered to save time.
Step 3: DFT groundstate calculation with a “coarse” mesh of k-points
- Perform a DFT groundstate calculation with a “coarse” mesh of k-points.
- This is the mesh of k-points that will be used in the subsequent ACFDT calculation.
- The following INCAR file is used (INCAR.DFT):
ISMEAR = 0 ; SIGMA = 0.05 EDIFF = 1E-8
- The following coarse KPOINTS file is used (KPOINTS.6):
6x6x6 0 G 6 6 6 0 0 0
Step 4: Obtain DFT "virtual" orbitals (empty states)
- Obtain DFT "virtual" orbitals (empty states).
- The following INCAR file is used in this step (INCAR.DIAG):
ALGO = Exact NBANDS = 64 NELM = 1 LOPTICS = .TRUE. ISMEAR = 0 ; SIGMA = 0.05
- In this step one needs to set LOPTICS=.TRUE. so that VASP calculates the derivative of the orbitals w.r.t. the Bloch wavevector (stored in the WAVEDER file). These are needed to correctly describe the long-wavelength limit of the dielectric screening.
- We use exact diagonalization (ALGO=Exact) and keep 64 bands after diagonalization (NBANDS=64).
- This calculations needs the orbitals (WAVECAR file) written in Step 3.
Step 5: calculate the RPA correlation energy (ACFDT)
- The following INCAR file is used in this step (INCAR.ACFDT):
ALGO = ACFDT NBANDS = 64 ISMEAR = 0 ; SIGMA = 0.05
- In OUTCAR.ACFDT.X.X one finds the RPA correlation energy, e.g.:
cutoff energy smooth cutoff RPA correlation Hartree contr. to MP2
---------------------------------------------------------------------------------
163.563 130.851 -10.7869840331 -19.0268026572
155.775 124.620 -10.7813600055 -19.0200457142
148.357 118.685 -10.7744584182 -19.0118291822
141.292 113.034 -10.7659931963 -19.0017871991
134.564 107.651 -10.7555712745 -18.9894197881
128.156 102.525 -10.7428704760 -18.9742991317
122.054 97.643 -10.7273118140 -18.9556871679
116.241 92.993 -10.7085991597 -18.9331679971
linear regression
converged value -10.9079580568 -19.1711146204
- Take the “converged value”, in this case: EC(RPA) = -10.9079580568eV (an approximate “infinite basis set” limit).
- This calculations needs the orbitals (WAVECAR file) and the derivative of the orbitals w.r.t. the Bloch wavevectors (WAVEDER file) written in Step 4.
- The RPA total energy is calculated as the, E(RPA)=EC(RPA)+EXX, the sum of the RPA correlation energy of step 5 EC(RPA) and the Hartree fock energy EXX of step 2.
- To get the Hartree fock energy
grep “free energy”in the OUTCAR.EXX.* file (there are two spaces between free and energy).
Running this example
The following bash-script doall.sh will run through all of the aforementioned calculational steps (step 1-5) for a range of different lattice constants (a=5.1-5.8 Å in steps of 0.1 Å)
#
# To run VASP this script calls $vasp_std
# (or posibly $vasp_gam and/or $vasp_ncl).
# These variables can be defined by sourcing vaspcmd
. vaspcmd 2> /dev/null
#
# When vaspcmd is not available and $vasp_std,
# $vasp_gam, and/or $vasp_ncl are not set as environment
# variables, you can specify them here
[ -z "`echo $vasp_std`" ] && vasp_std="mpirun -np 8 /path-to-your-vasp/vasp_std"
[ -z "`echo $vasp_gam`" ] && vasp_gam="mpirun -np 8 /path-to-your-vasp/vasp_gam"
[ -z "`echo $vasp_ncl`" ] && vasp_ncl="mpirun -np 8 /path-to-your-vasp/vasp_ncl"
#
# The real work starts here
#
for i in 5.1 5.2 5.3 5.4 5.5 5.6 5.7 5.8 ; do
cat >POSCAR <<!
system Si
$i
0.5 0.5 0.0
0.0 0.5 0.5
0.5 0.0 0.5
2
cart
0.00 0.00 0.00
0.25 0.25 0.25
!
# start with a PBE calculation with a lot of k-points (needed for EXX)
rm WAVECAR WAVEDER
cp KPOINTS.12 KPOINTS
cp INCAR.DFT INCAR
$vasp_std
cp OUTCAR OUTCAR.DFT.$i
e1=`awk '/free energy/ {print $5}' OUTCAR`
# get the HF energy with PBE orbitals
cp INCAR.EXX INCAR
$vasp_std
e2=`awk '/free energy/ {print $5}' OUTCAR`
cp OUTCAR OUTCAR.EXX.$i
# now a PBE calculation with less k-points
rm WAVECAR WAVEDER
cp KPOINTS.6 KPOINTS
cp INCAR.DFT INCAR
$vasp_std
# obtain virtual orbitals
cp INCAR.DIAG INCAR
$vasp_std
cp OUTCAR OUTCAR.DIAG.$i
cp WAVECAR WAVECAR.$i
cp WAVEDER WAVEDER.$i
## for metals
# cp INCAR.HFC INCAR
# $vasp_std
#
# cp OUTCAR OUTCAR.HFC.$i
# e3=`awk '/HF-correction/ {print $4}' OUTCAR`
# RPA correlation
cp INCAR.ACFDT INCAR
$vasp_std
cp OUTCAR OUTCAR.ACFDT.$i
e4=`awk '/converged value/ {print $3}' OUTCAR`
# echo $i $e1 $e2 $e3 $e4 >> summary
echo $i $e1 $e2 $e4 >> summary
done
To execute the aforementions script:
./doall.sh
- When everything is finished you can quickly visualize (with gnuplot) the total energy vs. lattice-constant curves for DFT and RPA by means of:
./plotall.sh