Wrap-around errors: Difference between revisions
No edit summary |
No edit summary |
||
| (12 intermediate revisions by 3 users not shown) | |||
| Line 2: | Line 2: | ||
Wrap around errors arise if the FFT meshes are not | Wrap around errors arise if the FFT meshes are not | ||
sufficiently large. It can be shown that no errors exist | sufficiently large. It can be shown that no errors exist | ||
if the FFT meshes contain all | if the FFT meshes contain all <math>\bold{G}</math> vectors up to <math>2 G_{\rm cut}</math>. | ||
[[File:Wrap errors spheres.png|350px|thumb|Fig. 1: Sphere intersections for <math>G_{\mathrm{cut}}</math>]] | |||
It can be shown that the charge density contains | It can be shown that the charge density contains | ||
components up to <math>2 G_{\ | components up to <math>2 G_{\mathrm{cut}}</math>, where <math>2 G_{\mathrm{cut}}</math> is | ||
the "longest" plane wave in the basis set: | the "longest" plane wave in the basis set: | ||
| Line 45: | Line 47: | ||
<math> | <math> | ||
\rho^{\mathrm{ps}}_\bold{G} \equiv | \rho^{\mathrm{ps}}_\bold{G} \equiv | ||
\frac{1}{\Omega} \int \langle\bold{r} | \rho^{\mathrm{ps}}| \bold{r}\rangle e^{-i \bold{G}\bold{r}}\, d \bold{r} \to \frac{1}{N_{\mathrm{FFT}}} \sum_{\bold{r}} \rho^{\mathrm{ps}}_{\bold{r}} e^{-i \bold{G}\bold{r}} | \frac{1}{\Omega} \int \langle\bold{r} | \rho^{\mathrm{ps}}| \bold{r}\rangle e^{-i \bold{G}\bold{r}}\, d \bold{r} \to \frac{1}{N_{\mathrm{FFT}}} \sum_{\bold{r}} \rho^{\mathrm{ps}}_{\bold{r}} e^{-i \bold{G}\bold{r}}. | ||
</math> | </math> | ||
{{ | Using the above equations for <math>\rho^{\mathrm{ps}}_{\bold{r}}</math> and <math>C_{\bold{r}n\bold{k}}</math> it | ||
is very easy to show that <math>\rho^{\mathrm{ps}}_{\bold{r}}</math> contains Fourier-components up | |||
to <math>2 G_{\mathrm{cut}}</math>. | |||
is very easy to show that | |||
to | |||
Generally it can be shown that | Generally it can be shown that | ||
a the convolution | a the convolution <math>f_r=f^1_r f^2_r</math> | ||
of two | of two functions <math>f^1_r</math> with Fourier-components | ||
up to | up to <math>G_1</math> and <math>f^2_r</math> with Fourier-components | ||
up to | up to <math>G_2</math> contains Fourier-components up to <math>G_1+G_2</math>. | ||
The property of the convolution comes once again into play, | The property of the convolution comes once again into play, | ||
when the action of the Hamiltonian onto a wavefunction is | when the action of the Hamiltonian onto a wavefunction is | ||
calculated. The action of the local-potential is given by | calculated. The action of the local-potential is given by | ||
<math> | |||
\ | a_{\bold{r}} = V_{\bold{r}} C_{\bold{r}n\bold{k}}. | ||
\ | </math> | ||
\ | |||
Only the components <math>a_{\bold{G}}</math> with <math>|\bold{G}| < G_{\mathrm{cut}}</math> are taken into | |||
The charge density contains components up to | account (see section {{TAG|ALGO}}: <math>a_{\bold{G}}</math> is added to the wavefunction | ||
the acceleration | during the iterative refinement of the wavefunctions <math>C_{\bold{G}n\bold{k}}</math>, | ||
and <math>C_{\bold{G}n\bold{k}}</math> contains only components up to <math>G_{\mathrm{cut}}</math>). | |||
From the previous theorem we see that <math>a_{\bold{r}}</math> contains | |||
components up to <math>3 G_{\mathrm{cut}}</math> (<math>V_{\bold{r}}</math> contains components up to | |||
<math>2 G_{\mathrm{cut}}</math>). | |||
If the FFT-mesh contains all components up to <math>2 G_{\mathrm cut}</math> | |||
the resulting wrap-around error is once again 0. This can | |||
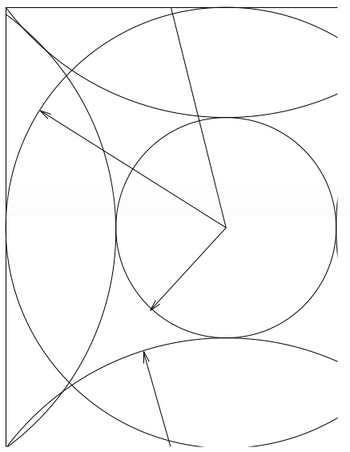
be easily seen in Fig. 1. Here we see that the small sphere contains all plane waves included in the basis set <math>G<G_{\mathrm{cut}}</math>. | |||
The charge density contains components up to <math>2 G_{\mathrm{cut}}</math> (second sphere), and | |||
the acceleration <math>a</math> components up to <math>3 G_{\mathrm{cut}}</math>, which are reflected | |||
in (third sphere) because of the finite size of the FFT-mesh. Nevertheless | in (third sphere) because of the finite size of the FFT-mesh. Nevertheless | ||
the components | the components <math>a_{\bold{G}}</math> with <math>| \bold{G}| < G_{\mathrm{cut}}</math> are correct i.e. | ||
the small sphere does not intersect with the third large sphere | the small sphere does not intersect with the third large sphere} | ||
---- | ---- | ||
[[Category:Electronic | [[Category:Electronic minimization]][[Category:Charge density]][[Category:Theory]] | ||
Latest revision as of 16:07, 6 April 2022
In this section we will discuss wrap around errors. Wrap around errors arise if the FFT meshes are not sufficiently large. It can be shown that no errors exist if the FFT meshes contain all vectors up to .
It can be shown that the charge density contains components up to , where is the "longest" plane wave in the basis set:
The wavefunction is defined as
and in real space it is given by
Using Fast Fourier transformations one can define
Therefore the wavefunction can be written in real space as
The charge density is simply given by
and in the reciprocal mesh it can be written as
Using the above equations for and it is very easy to show that contains Fourier-components up to .
Generally it can be shown that a the convolution of two functions with Fourier-components up to and with Fourier-components up to contains Fourier-components up to .
The property of the convolution comes once again into play, when the action of the Hamiltonian onto a wavefunction is calculated. The action of the local-potential is given by
Only the components with are taken into account (see section ALGO: is added to the wavefunction during the iterative refinement of the wavefunctions , and contains only components up to ). From the previous theorem we see that contains components up to ( contains components up to ).
If the FFT-mesh contains all components up to the resulting wrap-around error is once again 0. This can be easily seen in Fig. 1. Here we see that the small sphere contains all plane waves included in the basis set . The charge density contains components up to (second sphere), and the acceleration components up to , which are reflected in (third sphere) because of the finite size of the FFT-mesh. Nevertheless the components with are correct i.e. the small sphere does not intersect with the third large sphere}
