Pulay stress: Difference between revisions
| (242 intermediate revisions by the same user not shown) | |||
| Line 1: | Line 1: | ||
Pulay stress is unphysical stress resulting from unconverged calculations with respect to the basis set. It distorts the cell structure, decreasing it from the equilibrium volume and creating difficulties in volume relaxation. The resultant energy vs. volume curves, cf. Figure 1 (top), are jagged and special care must be taken to obtain reasonable structures, cf. [[volume relaxation|Volume relaxation]]. In this article, the computational origin of this is discussed. [[File:Pressure_energy_volume.png|400px|thumb|Figure 1. Total energy (left y-axis) and absolute pressure (right y-axis) vs. lattice parameter. Equilibrium lattice parameters for energy and pressure are shown. These coincide when Pulay stress is eliminated. ENCUT = 250 eV (top - unconverged) and 540 eV (bottom - converged). Diamond in a primitive cell - 2x2x2 k-point mesh.]]It is important to note that problems due to the Pulay stress can often be neglected if only volume-conserving relaxations are performed. This is because the Pulay stress is, usually, nearly uniform and only changes the diagonal elements of the stress tensor by a constant amount. | |||
= Introduction = | |||
The energy for a periodic system, e.g. band structures, is calculated using a finite number of plane waves and a finite number of k-points. A fixed number of plane waves or plane wave energy cutoff may be used to set a constant basis.{{cite|gomesdacosta:nielsen:kunc:1986}} In VASP, a constant energy cutoff is used, cf. {{TAG|ENCUT}}. The number of plane waves <b><i><span>N</span></b><sub>PW</sub></i> (Note: the number of plane waves in VASP can be found using by searching for ''NPLWV'' in the {{TAG|OUTCAR}} file) is related to the energy cutoff <b><i><span>E</span></b><sub>cutoff</sub></i> and the size of the cell <span>'''Ω'''</span><sub>0</sub>: | |||
::<math> N_{PW} \propto\ \Omega_0\ E_{cutoff}^{3/2} </math> | |||
<b><i><span>N</span></b><sub>PW</sub></i> is constant in a relaxation calculation, which means that <b><i><span>E</span></b><sub>cutoff</sub></i> must change to compensate for changes in <span>'''Ω'''</span><sub>0</sub>. All the initial G-vectors within a sphere are included in the basis. However, when comparing cells of different sizes, i.e. during a relaxation, the cell shape is relaxed, so the direct and reciprocal lattice vectors change. The number of reciprocal G-vectors in the basis is kept fixed but the length of the G-vectors changes, indirectly changing the energy cutoff. In other words, the shape of the cutoff region changes from a sphere to an ellipsoid. This can be solved by using an infinite number of k-points and plane waves. In practice, a large enough plane wave energy cutoff and number of k-points leads to converged energies.{{cite|payne:francis:1990}} All energy changes are strictly consistent with the stress tensor; however, when the basis set is too small, i.e. prematurely truncated, this results in discontinuities in the total energy between cells of varying volumes. These discontinuities between energy and volume create stress that decreases the equilibrium volume (cf. Fig. 1 (top)), due to the diagonal components of the stress tensor being incorrect. This is called the ''Pulay stress''. | |||
The pressure of the cell, being proportional to the trace of the stress tensor, can be used to visualize this. When the cell volume is below the equilibrium volume, the pressure is positive; contrastingly, it is negative when above the equilibrium volume, so at equilibrium, this is zero. Plotting the magnitude of the pressure vs. volume curve and the total energy allows comparison between these two minima. In Figure 1 it is clear that the the absolute pressure-volume and energy-volume minima coincide for a converged basis, while the pressure equilibrium is much lower than the energy equilibrium for the unconverged basis. This is the effect of the Pulay stress. | |||
== | = Further explanation = | ||
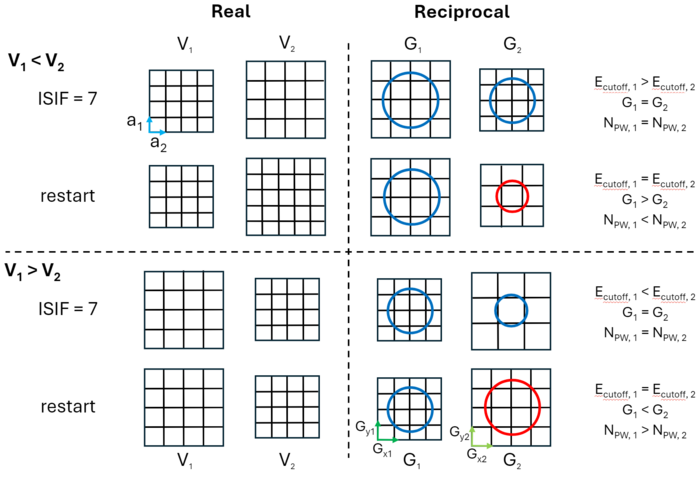
As mentioned previously, <b><i><span>N</span></b><sub>PW</sub></i> is constant in a relaxation calculation, which means that <b><i><span>E</span></b><sub>cutoff</sub></i> must change to compensate for changes in <span>'''Ω'''</span><sub>0</sub>. This is illustrated in Fig. 2. The initial G-vectors within a sphere are included within the basis. | |||
When the cell volume increases (<b><span>V</span></b><sub>1</sub> < <b><span>V</span></b><sub>1</sub>), the number of G-vectors in reciprocal space remains constant, but their length increases (cf. Fig. 2 (top)). This effectively results in a change of basis, leading to (<b><i><span>E</span></b><sub>cutoff, 1</sub></i> > <b><i><span>E</span></b><sub>cutoff, 2</sub></i>). This basis remains constant for the duration of the relaxation. However, if the calculation is then restarted, the basis is reset. This means that the number of G-vectors is greater for the larger, real-space cell. One effect of this is that there are more real-space grid points. However, the corresponding reciprocal space decreases. | |||
Contrastingly, see Fig. 2 (bottom), when the volume decreases on relaxation (<b><span>V</span></b><sub>1</sub> > <b><span>V</span></b><sub>1</sub>), the length of the G-vectors decreases. The effective <b><i><span>E</span></b><sub>cutoff</sub></i> should increase but this does not improve the situation, as it creates an artificial pressure. The reciprocal space grid points are effectively sparser. If the calculation restarts, the basis is reset, so the number of G-vectors decreases for the smaller real space cell. | |||
[[File:Pulay_stress_grids.png|700px|thumb|centre|Figure 2. Cell shape and lattice positions are kept constant, while the volume <b><span>V</span></b> is free to change (ISIF = 7). The initial volume <b><span>V</span></b><sub>1</sub> changes to the final volume <b><span>V</span></b><sub>2</sub>. Two cases are given, one for volume increasing on relaxation (top) and one for it decreasing (bottom). The change in real space is given on the left, while the change in reciprocal space and the subsequent effect on the G-vectors is given on the right. Blue is the initial basis, while red is the new, restarted basis. The relation between <b><i><span>E</span></b><sub>cutoff</sub></i>, <b><i><span>N</span></b><sub>PW</sub></i>, and G-vectors is given for the initial and final volumes.]] | |||
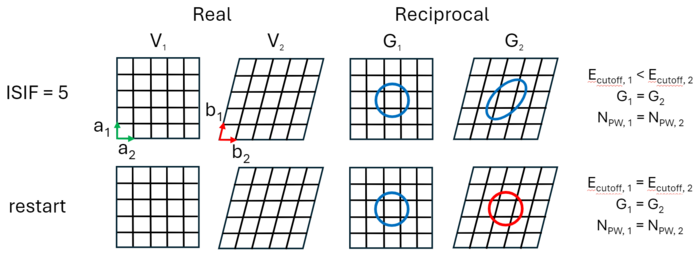
Alternatively, the shape of the cell could change. As the shape changes, the G-vectors continue to be directed along the lattice coordinates, meaning that some shorten while others lengthen, see Fig. 3. This results in a shift from a spherical basis, where all G-vectors are of equal length, to one where some are stretched and others compressed, i.e. an ellipsoid. This changes the effective <b><i><span>E</span></b><sub>cutoff</sub></i> along each lattice parameter. On resetting the calculation, the cutoff is once again spherical. This draws an analogy to the symmetry breaking of the Bravais lattice seen for gradient-corrected functionals (cf. {{TAG|GGA_COMPAT}}), where the spherical symmetry of the G-vectors is broken for non-cubic cells. | |||
[[File:Shape_pulay_grids.png|700px|thumb|centre|Figure 3. Cell volume and lattice positions are kept constant, while the shape is free to change (ISIF = 5). The shape changes from cubic to hexagonal. The blue spherical basis changes to the red ellipsoid basis, along the direction of the sheer. On restarting, a spherical basis returns.]] | |||
[[Category:Ionic minimization]][[Category:Howto]] | |||
==References== | ==References== | ||
Latest revision as of 09:11, 30 August 2024
Pulay stress is unphysical stress resulting from unconverged calculations with respect to the basis set. It distorts the cell structure, decreasing it from the equilibrium volume and creating difficulties in volume relaxation. The resultant energy vs. volume curves, cf. Figure 1 (top), are jagged and special care must be taken to obtain reasonable structures, cf. Volume relaxation. In this article, the computational origin of this is discussed.
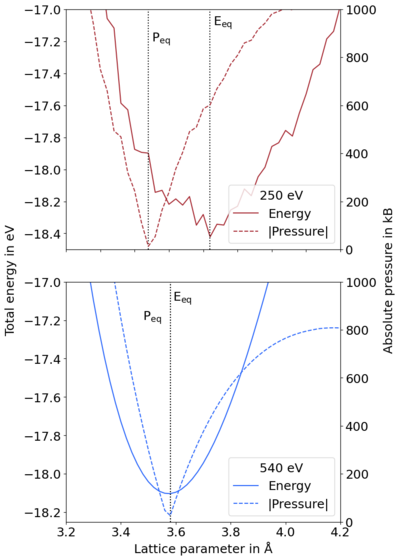
It is important to note that problems due to the Pulay stress can often be neglected if only volume-conserving relaxations are performed. This is because the Pulay stress is, usually, nearly uniform and only changes the diagonal elements of the stress tensor by a constant amount.
Introduction
The energy for a periodic system, e.g. band structures, is calculated using a finite number of plane waves and a finite number of k-points. A fixed number of plane waves or plane wave energy cutoff may be used to set a constant basis.[1] In VASP, a constant energy cutoff is used, cf. ENCUT. The number of plane waves NPW (Note: the number of plane waves in VASP can be found using by searching for NPLWV in the OUTCAR file) is related to the energy cutoff Ecutoff and the size of the cell Ω0:
NPW is constant in a relaxation calculation, which means that Ecutoff must change to compensate for changes in Ω0. All the initial G-vectors within a sphere are included in the basis. However, when comparing cells of different sizes, i.e. during a relaxation, the cell shape is relaxed, so the direct and reciprocal lattice vectors change. The number of reciprocal G-vectors in the basis is kept fixed but the length of the G-vectors changes, indirectly changing the energy cutoff. In other words, the shape of the cutoff region changes from a sphere to an ellipsoid. This can be solved by using an infinite number of k-points and plane waves. In practice, a large enough plane wave energy cutoff and number of k-points leads to converged energies.[2] All energy changes are strictly consistent with the stress tensor; however, when the basis set is too small, i.e. prematurely truncated, this results in discontinuities in the total energy between cells of varying volumes. These discontinuities between energy and volume create stress that decreases the equilibrium volume (cf. Fig. 1 (top)), due to the diagonal components of the stress tensor being incorrect. This is called the Pulay stress.
The pressure of the cell, being proportional to the trace of the stress tensor, can be used to visualize this. When the cell volume is below the equilibrium volume, the pressure is positive; contrastingly, it is negative when above the equilibrium volume, so at equilibrium, this is zero. Plotting the magnitude of the pressure vs. volume curve and the total energy allows comparison between these two minima. In Figure 1 it is clear that the the absolute pressure-volume and energy-volume minima coincide for a converged basis, while the pressure equilibrium is much lower than the energy equilibrium for the unconverged basis. This is the effect of the Pulay stress.
Further explanation
As mentioned previously, NPW is constant in a relaxation calculation, which means that Ecutoff must change to compensate for changes in Ω0. This is illustrated in Fig. 2. The initial G-vectors within a sphere are included within the basis.
When the cell volume increases (V1 < V1), the number of G-vectors in reciprocal space remains constant, but their length increases (cf. Fig. 2 (top)). This effectively results in a change of basis, leading to (Ecutoff, 1 > Ecutoff, 2). This basis remains constant for the duration of the relaxation. However, if the calculation is then restarted, the basis is reset. This means that the number of G-vectors is greater for the larger, real-space cell. One effect of this is that there are more real-space grid points. However, the corresponding reciprocal space decreases.
Contrastingly, see Fig. 2 (bottom), when the volume decreases on relaxation (V1 > V1), the length of the G-vectors decreases. The effective Ecutoff should increase but this does not improve the situation, as it creates an artificial pressure. The reciprocal space grid points are effectively sparser. If the calculation restarts, the basis is reset, so the number of G-vectors decreases for the smaller real space cell.
Alternatively, the shape of the cell could change. As the shape changes, the G-vectors continue to be directed along the lattice coordinates, meaning that some shorten while others lengthen, see Fig. 3. This results in a shift from a spherical basis, where all G-vectors are of equal length, to one where some are stretched and others compressed, i.e. an ellipsoid. This changes the effective Ecutoff along each lattice parameter. On resetting the calculation, the cutoff is once again spherical. This draws an analogy to the symmetry breaking of the Bravais lattice seen for gradient-corrected functionals (cf. GGA_COMPAT), where the spherical symmetry of the G-vectors is broken for non-cubic cells.
References
- ↑ P. Gomes Dacosta, O. Nielsen, and K. Kunc, Stress theorem in the determination of static equilibrium by the density functional method, J. Phys. C: Solid State Phys. 19, 3163 (1986).
- ↑ G. P. Francis and M. C. Payne, Finite basis set corrections to total energy pseudopotential calculations, J. Condens. Matter Phys. 2, 4395 (1990).
