Computing the phonon dispersion and DOS: Difference between revisions
(Remove statement about older version of VASP) |
(→Polar materials: Expand section, give more details for how to set dielectric properties and show examples of LO-TO splitting) |
||
| (10 intermediate revisions by 2 users not shown) | |||
| Line 1: | Line 1: | ||
After computing the force constants using the [[Phonons_from_finite_differences|finite differences]] or [[Phonons_from_density-functional-perturbation_theory|density functional perturbation theory]] approaches, it is possible to compute the phonon dispersion | After computing the force constants using the [[Phonons_from_finite_differences|finite differences]] or [[Phonons_from_density-functional-perturbation_theory|density-functional-perturbation theory]] (DFPT) approaches, it is possible to compute the phonon dispersion relation as well as the phonon density of states (DOS). | ||
This is accomplished by Fourier interpolating the interatomic force constants from a supercell calculation to the primitive cell. | |||
== Phonon dispersion: Step-by-step instructions == | == Phonon dispersion: Step-by-step instructions == | ||
=== Step 1: Compute the force constants | === Step 1: Compute the force constants === | ||
There are two possible approaches for computing the force constants and then building the dynamical matrix: | There are two possible approaches for computing the force constants and then building the dynamical matrix: | ||
# Using [[Phonons_from_finite_differences|finite differences]] with | # Using [[Phonons_from_finite_differences|finite differences]] with {{TAGO|IBRION|5, 6}}. | ||
# Using [[Phonons_from_density-functional-perturbation_theory| | # Using [[Phonons_from_density-functional-perturbation_theory|DFPT]] with {{TAGO|IBRION|7, 8}}. | ||
These calculations must be performed in a supercell so that the force constants vanish at large distances. | |||
{{NB|important|The phonon frequencies need to be converged with respect to the supercell size.}} | |||
=== Step 2: Provide | === Step 2: Provide '''q'''-points along a high-symmetry path === | ||
Create a {{FILE|QPOINTS}} file containing a '''q'''-points path at which the phonon dispersion | Create a {{FILE|QPOINTS}} file containing a '''q'''-points path at which the phonon dispersion is computed. | ||
This is accomplished using the [[KPOINTS#Band-structure calculations|line mode]] of the {{FILE|KPOINTS}}-file format. | |||
=== Step 3: Compute the phonon dispersion | === Step 3: Compute the phonon dispersion === | ||
To | To compute the phonon dispersion, set {{TAGO|LPHON_DISPERSION|true}} in the {{FILE|INCAR}} file. | ||
The amount of information written to the {{FILE|OUTCAR}} file can be tuned using the {{TAG|PHON_NWRITE}} tag. | |||
=== Reading of force constants === | |||
Steps 1-3 can be performed in one VASP calculation. | |||
However, generating the finite displacements in the supercell to compute force constants is time-consuming. | |||
It is possible to skip that step by providing force constants from a previous run. | |||
Rename the {{FILE|vaspout.h5}} output file from the previous calculation to {{FILE|vaspin.h5}}, set | |||
{{TAGBL|LPHON_READ_FORCE_CONSTANTS}} = True | |||
{{TAGBL|LPHON_DISPERSION}} = True | |||
and provide a {{FILE|QPOINTS}} file. | |||
== Phonon DOS: Step-by-step instructions == | |||
== Phonon | === Step 1: Compute the force constants === | ||
Same as [[#Phonon dispersion: Step-by-step instructions#Step 1: Compute the force constants|above]]. | |||
This can be skipped by providing force constants in {{FILE|vaspin.h5}} and setting {{TAGO|LPHON_READ_FORCE_CONSTANTS|True}}. | |||
=== Step 2: Specify a uniform '''q'''-point mesh === | |||
=== Step 2: Specify a uniform '''q'''-point mesh | |||
Create a {{FILE|QPOINTS}} file that specifies a sufficiently dense, uniform '''q'''-point mesh. | Create a {{FILE|QPOINTS}} file that specifies a sufficiently dense, uniform '''q'''-point mesh. | ||
=== Step 3: Compute the | === Step 3: Compute the DOS === | ||
Set {{ | Set {{TAGO|PHON_DOS|0|op=>}} in the {{FILE|INCAR}} file. The DOS is computed between | ||
<math>[\omega_{\text{min}}-5\sigma,\omega_{\text{max}}+5\sigma]</math> with | <math>[\omega_{\text{min}}-5\sigma,\omega_{\text{max}}+5\sigma]</math> with | ||
<math>\omega_{\text{min}}</math> and | <math>\omega_{\text{min}}</math> and | ||
| Line 40: | Line 48: | ||
<math>\sigma</math> the broadening ({{TAG|PHON_SIGMA}}). | <math>\sigma</math> the broadening ({{TAG|PHON_SIGMA}}). | ||
The number of energy points in this energy range is specified by the {{TAG|PHON_NEDOS}} tag. To use a Gaussian-smearing method for the computation of the DOS set {{ | The number of energy points in this energy range is specified by the {{TAG|PHON_NEDOS}} tag. To use a Gaussian-smearing method for the computation of the DOS set {{TAGO|PHON_DOS|1}} or to use the tetrahedron method set {{TAGO|PHON_DOS|2}}. | ||
== Polar materials == | |||
If the material is polar, i.e., two or more atoms in the unit cell carry non-zero Born effective charge tensors, the long-range dipole-dipole interaction has to be treated by [[Phonons:_Theory#Long-range_interatomic_force_constants_.28LO-TO_splitting.29|Ewald summation]]. | |||
This is achieved by setting {{TAGO|LPHON_POLAR|True}}, supplying the static dielectric tensor ({{TAG|PHON_DIELECTRIC}}) and the Born-effective charges ({{TAG|PHON_BORN_CHARGES}}). | |||
The values for these dielectric properties have to be obtained from a separate VASP calculation in the unit cell setting {{TAG|LEPSILON}} or {{TAG|LCALCEPS}}. | |||
{{NB|important|Make sure to properly converge this unit-cell calculation with respect to the k-point mesh ({{FILE|KPOINTS}}) and the electronic cutoff energy ({{TAG|ENCUT}}) since the optical phonon frequencies depend strongly on the dielectric properties.}} | |||
Optionally, specify a reciprocal space cutoff radius ({{TAG|PHON_G_CUTOFF}}) for the Ewald summation. | |||
=== Obtaining the dielectric properties === | |||
After a successful linear-response calculation using either {{TAG|LEPSILON}} or {{TAG|LCALCEPS}}, VASP writes the Born effective charge tensor and the ion-clamped static dielectric tensor to {{FILE|OUTCAR}}, {{FILE|vasprun.xml}} and {{FILE|vaspout.h5}}. | |||
{{NB|mind|The {{FILE|vaspout.h5}} file is only available if VASP is compiled with [[:Category:HDF5 support|HDF5 support]].}} | |||
Here is an example output for a system consisting of two atoms per cell (MgO) in the {{FILE|OUTCAR}} file: | |||
<pre> | |||
MACROSCOPIC STATIC DIELECTRIC TENSOR (including local field effects in DFT) | |||
------------------------------------------------------ | |||
3.130368 -0.000000 -0.000000 | |||
0.000000 3.130368 0.000000 | |||
-0.000000 0.000000 3.130368 | |||
</pre> | |||
and | |||
<pre> | |||
BORN EFFECTIVE CHARGES (including local field effects) (in |e|, cummulative output) | |||
--------------------------------------------------------------------------------- | |||
ion 1 | |||
1 1.97026 0.00000 -0.00000 | |||
2 -0.00000 1.97026 0.00000 | |||
3 -0.00000 0.00000 1.97026 | |||
ion 2 | |||
1 -1.97026 -0.00000 0.00000 | |||
2 0.00000 -1.97026 -0.00000 | |||
3 0.00000 -0.00000 -1.97026 | |||
</pre> | |||
The corresponding XML entries in the {{FILE|vasprun.xml}} file can be queried with the following XPath queries: | |||
<pre> | |||
/modeling/calculation/array[@name="born_charges"] | |||
/modeling/calculation/varray[@name="dielectric_dft"] | |||
</pre> | |||
Finally, the same information is also available in the {{FILE|vaspout.h5}} binary file at the following dataset locations: | |||
<pre> | |||
results/born_charges/born_charges | |||
results/dielectric/dielectric_dft | |||
</pre> | |||
=== Specifying the dielectric properties as input === | |||
Once the Born effective charges and the ion-clamped static dielectric tensor have been retrieved, they need to be specified in the {{FILE|INCAR}} file of the supercell calculation via their respective tags ({{TAG|PHON_BORN_CHARGES}} and {{TAG|PHON_DIELECTRIC}}). | |||
Each tensor is specified row by row as a list of real numbers. | |||
Line breaks can optionally be inserted using the "<tt>\</tt>" character to improve readability. | |||
For example, the values from the MgO calculation above could be specified as follows: | |||
<pre> | |||
PHON_DIELECTRIC = \ | |||
3.13036840 -0.00000000 -0.00000000 \ | |||
0.00000000 3.13036840 0.00000000 \ | |||
-0.00000000 0.00000000 3.13036840 | |||
PHON_BORN_CHARGES = \ | |||
1.97025920 -0.00000000 -0.00000000 \ | |||
0.00000000 1.97025920 0.00000000 \ | |||
-0.00000000 0.00000000 1.97025920 \ | |||
\ | |||
-1.97025920 0.00000000 0.00000000 \ | |||
-0.00000000 -1.97025920 -0.00000000 \ | |||
0.00000000 -0.00000000 -1.97025920 | |||
</pre> | |||
=== LO-TO splitting === | |||
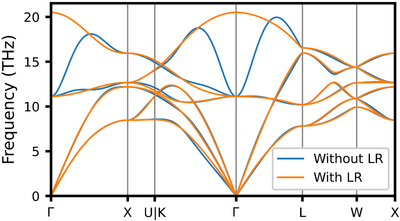
[[Image:MgO-phonons-LR-comparison.png|400px|thumb|Phonon dispersion relation of MgO (rock-salt) comparing calculations with and without long-range (LR) dipole corrections. Notice the strong splitting of frequencies at the Γ-point.]] | |||
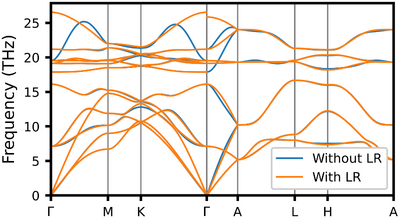
[[Image:AlN-phonons-LR-comparison.png|400px|thumb|Phonon dispersion relation of AlN (wurtzite) comparing calculations with and without long-range (LR) dipole corrections. Notice the discontinuities around the Γ-point.]] | |||
As described on the [[Phonons:_Theory#Long-range_interatomic_force_constants_.28LO-TO_splitting.29|theory page]], the presence of long-range electrostatic interactions leads to the splitting of the longitudinal optical (LO) from the transverse optical (TO) phonon modes. | |||
Once the required dielectric properties are provided and {{TAGO|LPHON_POLAR|True}} is set, VASP automatically considers the long-range dipole-dipole contributions to the interatomic force constants for phonon calculations. | |||
To illustrate the importance of long-range dipole corrections, we show two calculations of phonons in polar materials with strong LO-TO splitting. | |||
First is MgO, which forms an ionic rock-salt crystal structure (face-centered cubic). | |||
The corresponding figure shows a comparison against a calculation that does not include the long-range dipole corrections. | |||
Both calculations were performed in a <tt>4x4x4</tt> supercell with only the Γ-point in the k-point mesh. | |||
In the case of MgO, the magnitude of the LO-TO splitting is considerably large, on the same order of magnitude as the LO phonon frequencies. | |||
Notice also the improved smoothness of the phonon bands when long-range corrections are included. | |||
Otherwise the interpolation procedure is prone to overshooting, resulting in unwanted oscillations. | |||
The second example is AlN in the hexagonal wurtzite structure. | |||
This structure is less isotropic than the rock-salt structure of MgO. | |||
In this case, the Born effective charges and dielectric constants associated with different spatial directions can be different. | |||
The phonon frequencies obtained by including the long-range dipole corrections are therefore more dependent on the direction of the phonon wave vector, <math>\mathbf{q}</math>. | |||
This results in discontinuities around the Γ-point when <math>\mathbf{q} \to \mathbf{0}</math>, as shown in the accompanying figure. | |||
==Related tags and articles== | ==Related tags and articles== | ||
Latest revision as of 15:31, 23 February 2024
After computing the force constants using the finite differences or density-functional-perturbation theory (DFPT) approaches, it is possible to compute the phonon dispersion relation as well as the phonon density of states (DOS). This is accomplished by Fourier interpolating the interatomic force constants from a supercell calculation to the primitive cell.
Phonon dispersion: Step-by-step instructions
Step 1: Compute the force constants
There are two possible approaches for computing the force constants and then building the dynamical matrix:
- Using finite differences with
IBRION = 5, 6. - Using DFPT with
IBRION = 7, 8.
These calculations must be performed in a supercell so that the force constants vanish at large distances.
| Important: The phonon frequencies need to be converged with respect to the supercell size. |
Step 2: Provide q-points along a high-symmetry path
Create a QPOINTS file containing a q-points path at which the phonon dispersion is computed. This is accomplished using the line mode of the KPOINTS-file format.
Step 3: Compute the phonon dispersion
To compute the phonon dispersion, set LPHON_DISPERSION = true in the INCAR file.
The amount of information written to the OUTCAR file can be tuned using the PHON_NWRITE tag.
Reading of force constants
Steps 1-3 can be performed in one VASP calculation. However, generating the finite displacements in the supercell to compute force constants is time-consuming. It is possible to skip that step by providing force constants from a previous run. Rename the vaspout.h5 output file from the previous calculation to vaspin.h5, set
LPHON_READ_FORCE_CONSTANTS = True LPHON_DISPERSION = True
and provide a QPOINTS file.
Phonon DOS: Step-by-step instructions
Step 1: Compute the force constants
Same as above.
This can be skipped by providing force constants in vaspin.h5 and setting LPHON_READ_FORCE_CONSTANTS = True.
Step 2: Specify a uniform q-point mesh
Create a QPOINTS file that specifies a sufficiently dense, uniform q-point mesh.
Step 3: Compute the DOS
Set PHON_DOS > 0 in the INCAR file. The DOS is computed between
with
and
the lowest and highest phonon frequency and
the broadening (PHON_SIGMA).
The number of energy points in this energy range is specified by the PHON_NEDOS tag. To use a Gaussian-smearing method for the computation of the DOS set PHON_DOS = 1 or to use the tetrahedron method set PHON_DOS = 2.
Polar materials
If the material is polar, i.e., two or more atoms in the unit cell carry non-zero Born effective charge tensors, the long-range dipole-dipole interaction has to be treated by Ewald summation.
This is achieved by setting LPHON_POLAR = True, supplying the static dielectric tensor (PHON_DIELECTRIC) and the Born-effective charges (PHON_BORN_CHARGES).
The values for these dielectric properties have to be obtained from a separate VASP calculation in the unit cell setting LEPSILON or LCALCEPS.
| Important: Make sure to properly converge this unit-cell calculation with respect to the k-point mesh (KPOINTS) and the electronic cutoff energy (ENCUT) since the optical phonon frequencies depend strongly on the dielectric properties. |
Optionally, specify a reciprocal space cutoff radius (PHON_G_CUTOFF) for the Ewald summation.
Obtaining the dielectric properties
After a successful linear-response calculation using either LEPSILON or LCALCEPS, VASP writes the Born effective charge tensor and the ion-clamped static dielectric tensor to OUTCAR, vasprun.xml and vaspout.h5.
| Mind: The vaspout.h5 file is only available if VASP is compiled with HDF5 support. |
Here is an example output for a system consisting of two atoms per cell (MgO) in the OUTCAR file:
MACROSCOPIC STATIC DIELECTRIC TENSOR (including local field effects in DFT)
------------------------------------------------------
3.130368 -0.000000 -0.000000
0.000000 3.130368 0.000000
-0.000000 0.000000 3.130368
and
BORN EFFECTIVE CHARGES (including local field effects) (in |e|, cummulative output)
---------------------------------------------------------------------------------
ion 1
1 1.97026 0.00000 -0.00000
2 -0.00000 1.97026 0.00000
3 -0.00000 0.00000 1.97026
ion 2
1 -1.97026 -0.00000 0.00000
2 0.00000 -1.97026 -0.00000
3 0.00000 -0.00000 -1.97026
The corresponding XML entries in the vasprun.xml file can be queried with the following XPath queries:
/modeling/calculation/array[@name="born_charges"] /modeling/calculation/varray[@name="dielectric_dft"]
Finally, the same information is also available in the vaspout.h5 binary file at the following dataset locations:
results/born_charges/born_charges results/dielectric/dielectric_dft
Specifying the dielectric properties as input
Once the Born effective charges and the ion-clamped static dielectric tensor have been retrieved, they need to be specified in the INCAR file of the supercell calculation via their respective tags (PHON_BORN_CHARGES and PHON_DIELECTRIC). Each tensor is specified row by row as a list of real numbers. Line breaks can optionally be inserted using the "\" character to improve readability. For example, the values from the MgO calculation above could be specified as follows:
PHON_DIELECTRIC = \
3.13036840 -0.00000000 -0.00000000 \
0.00000000 3.13036840 0.00000000 \
-0.00000000 0.00000000 3.13036840
PHON_BORN_CHARGES = \
1.97025920 -0.00000000 -0.00000000 \
0.00000000 1.97025920 0.00000000 \
-0.00000000 0.00000000 1.97025920 \
\
-1.97025920 0.00000000 0.00000000 \
-0.00000000 -1.97025920 -0.00000000 \
0.00000000 -0.00000000 -1.97025920
LO-TO splitting
As described on the theory page, the presence of long-range electrostatic interactions leads to the splitting of the longitudinal optical (LO) from the transverse optical (TO) phonon modes.
Once the required dielectric properties are provided and LPHON_POLAR = True is set, VASP automatically considers the long-range dipole-dipole contributions to the interatomic force constants for phonon calculations.
To illustrate the importance of long-range dipole corrections, we show two calculations of phonons in polar materials with strong LO-TO splitting. First is MgO, which forms an ionic rock-salt crystal structure (face-centered cubic). The corresponding figure shows a comparison against a calculation that does not include the long-range dipole corrections. Both calculations were performed in a 4x4x4 supercell with only the Γ-point in the k-point mesh. In the case of MgO, the magnitude of the LO-TO splitting is considerably large, on the same order of magnitude as the LO phonon frequencies. Notice also the improved smoothness of the phonon bands when long-range corrections are included. Otherwise the interpolation procedure is prone to overshooting, resulting in unwanted oscillations.
The second example is AlN in the hexagonal wurtzite structure. This structure is less isotropic than the rock-salt structure of MgO. In this case, the Born effective charges and dielectric constants associated with different spatial directions can be different. The phonon frequencies obtained by including the long-range dipole corrections are therefore more dependent on the direction of the phonon wave vector, . This results in discontinuities around the Γ-point when , as shown in the accompanying figure.
Related tags and articles
QPOINTS, LPHON_DISPERSION, PHON_NWRITE, LPHON_POLAR, PHON_DIELECTRIC, PHON_BORN_CHARGES, PHON_G_CUTOFF
