Nuclephile Substitution CH3Cl - mMD1: Difference between revisions
| (One intermediate revision by the same user not shown) | |||
| Line 71: | Line 71: | ||
== Calculation == | == Calculation == | ||
As in the previous example ({{TAG|Nucleophile Substitution CH3Cl - Standard MD}}) the reaction coordinate, the difference between two C-Cl distances, is monitored. Expected values for reactant: <math>\approx 1 \AA</math>, for product: <math>~-1 \AA</math>, for transition state: <math> 0 \AA </math>. | |||
| Line 121: | Line 121: | ||
===Expectation=== | ===Expectation=== | ||
The meta dynamics simulation pushes the system against the reaction barrier. The amplitude of oscillation of the collective variable increases (as a larger and larger region of configuration space is visited) and at some point the collective variable switches from a positive value (corresponding to the reactant) to a negative value (corresponding to the product). | The meta dynamics simulation pushes the system against the reaction barrier. The amplitude of oscillation of the collective variable increases (as a larger and larger region of configuration space is visited) and at some point the collective variable switches from a positive value (corresponding to the reactant) to a negative value (corresponding to the product). | ||
===Reality=== | ===Reality=== | ||
| Line 142: | Line 141: | ||
== Download == | == Download == | ||
[ | [[Media:CH3Cl_mMD1.tgz| CH3Cl_mMD1.tgz]] | ||
{{Template:Molecular dynamics - Tutorial}} | {{Template:Molecular dynamics - Tutorial}} | ||
[[Category:Examples]] | [[Category:Examples]] | ||
Latest revision as of 09:45, 14 November 2019
Task
In this example a nucleophile substitution of a Cl- by another Cl- in CH3Cl is attempted via a meta dynamics calculation.
Input
POSCAR
1.00000000000000
12.0000000000000000 0.0000000000000000 0.0000000000000000
0.0000000000000000 12.0000000000000000 0.0000000000000000
0.0000000000000000 0.0000000000000000 12.0000000000000000
C H Cl
1 3 2
cart
5.91331371 7.11364924 5.78037960
5.81982231 8.15982106 5.46969017
4.92222130 6.65954232 5.88978969
6.47810398 7.03808479 6.71586385
4.32824726 8.75151396 7.80743202
6.84157897 6.18713289 4.46842049
- The starting POSCAR file for this example can be found under POSCAR.init. It will be needed for the script that runs the job (run.sh).
- A sufficiently large cell is chosen to minimize the interactions between neighbouring cells and hence to simulate an isolated molecular reaction.
KPOINTS
Automatic 0 Gamma 1 1 1 0. 0. 0.
- For isolated atoms and molecules interactions between periodic images are negligible (in sufficiently large cells) hence no Brillouin zone sampling is necessary.
INCAR
PREC=Low EDIFF=1e-6 LWAVE=.FALSE. LCHARG=.FALSE. NELECT=22 NELMIN=4 LREAL=.FALSE. ALGO=VeryFast ISMEAR=-1 SIGMA=0.0516 ############################# MD setting ##################################### IBRION=0 # MD simulation NSW=50000 # number of steps POTIM=1 # integration step TEBEG=600 # simulation temperature MDALGO=11 # metaDynamics with Andersen thermostat ANDERSEN_PROB=0.10 # collision probability HILLS_BIN=50 # update the time-dependent bias # potential every 50 steps HILLS_H=0.005 # height of the Gaussian HILLS_W=0.05 # width of the Gaussian ##############################################################################
- The INCAR file in this example is the same as in the previous example (Nucleophile Substitution CH3Cl - Standard MD) with the exception of the metadynamics tags HILLS_H and HILLS_W.
- Metadynamics molecular dynamics is formally exact in the limit of infinitesimally small hills (HILLS_H) and infinite update time (HILLS_BIN) for the time-dependent bias potential, hence the parameter [[]] should be as small as possible while HILLS_BIN should be as large as possible.
- A random seed for reproducibility is used in this calculations which is added later by the run script.
- Meta dynamics is formally exact in the limit of infinitesimally small hills and infinite update times for the time-dependent bias potential. Hence the parameter HILLS_H should be as small as possible while HILLS_BIN should be as large as possible.
ICONST
For this example an ICONST file is used which looks like:
R 1 5 0 R 1 6 0 S 1 -1 5
- This file is the same as in the previous example Nucleophile Substitution CH3Cl - Standard MD with the exception that the 5 at the fourth entry in the third row specifies that a bias potential is applied to the special coordinate.
Calculation
As in the previous example (Nucleophile Substitution CH3Cl - Standard MD) the reaction coordinate, the difference between two C-Cl distances, is monitored. Expected values for reactant: , for product: , for transition state: .
Running the calculation
The mass for hydrogen in this example is set 3.016 a.u. corresponding to the tritium isotope. This way larger timesteps can be chosen for the MD. For practical reasons, we split our (pressumably long) meta dynamics calculation into shorter runs of length of 1000 fs for each (NSW=1000 and POTIM=1). At the end of each run, the HILLSPOT file (containing the bias potential generated in the previous run) must be copied to the PENALTYPOT file (the input file with bias potential). Meta dynamics is a fully stochastic simulation, the results can depend on the random numbers used in the calculations. To ensure best reproducibility the calculation is started from the same random seed (rseed="RANDOM_SEED = 311137787 0 0"). After each step the last random seed is copied to the INCAR file for the new step. This way reproducability is ensured between each step.
The calculation is executed using the "run" script:
#!/bin/bash runvasp="mpirun -np x executable_path" # ensure that this sequence of MD runs is reproducible cp POSCAR.init POSCAR cp INCAR.init INCAR rseed="RANDOM_SEED = 311137787 0 0" echo $rseed >> INCAR i=1 while [ $i -le 50 ] do # start vasp $runvasp # ensure that this sequence of MD runs is reproducible rseed=$(grep RANDOM_SEED REPORT |tail -1) cp INCAR.init INCAR echo $rseed >> INCAR # use bias potential generated in previous mMD run cp HILLSPOT PENALTYPOT # use the last configuration generated in the previous # run as initial configuration for the next run cp CONTCAR POSCAR # backup some important files cp REPORT REPORT.$i cp vasprun.xml vasprun.xml.$i let i=i+1 done
- The user has to adjust the runvasp variable, which holds the command for the executable command.
- Please run this script by typing:
bash ./run
Expectation
The meta dynamics simulation pushes the system against the reaction barrier. The amplitude of oscillation of the collective variable increases (as a larger and larger region of configuration space is visited) and at some point the collective variable switches from a positive value (corresponding to the reactant) to a negative value (corresponding to the product).
Reality
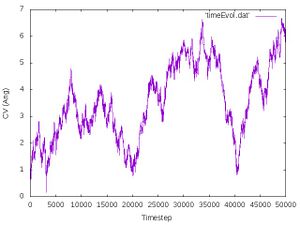
Most likely the collective variable increases to unexpectedly large values () while the transition region (around ) is either not sampled or it is smpled only in the final part of the simulation. In other words, the simulation spent most of its time sampling an uninteresting part of the configuration space related to the dissociation of the vdW complex instead pushing the configuration over the barrier. This is because meta dynamics always seeks for the path of least resistance. In the case of our model system this corresponds to the dissociation of the vdW complex because the barrier this process is much lower than that for the SN2 reaction.
To verify this the time evolution of the collective variable is monitored (and written to timeEvol.dat) by calling the command:
bash ../timeEv.sh
The time evolution is visualized using the command:
gnuplot -e "set terminal jpeg; set xlabel 'Timestep'; set ylabel 'CV (Ang)'; set style data lines; plot 'timeEvol.dat'" > timeEvol.jpg
It should look like the following:
We indeed see that the transition region is never sampled and that the meta dynamics simulation takes the path of least resistance, which is the dissociation of the vdW complex.
Solution
In order to restrict the sampling into the part of configuration space that is relevant for the process of interest (say between and ) we must use some trick which is explained in the next example.