Dielectric properties of Si using BSE: Difference between revisions
No edit summary |
|||
| (23 intermediate revisions by 2 users not shown) | |||
| Line 1: | Line 1: | ||
Description: | {{Template:BSE - Tutorial}} | ||
== Task == | |||
Description: Calculate the dielectric function of Si including excitonic effects by solving the Bethe-Salpeter equation (BSE) on top of GW0. | |||
== Input == | |||
=== {{FILE|POSCAR}} === | |||
Si | |||
5.4300 | |||
0.5 0.5 0.0 | |||
0.0 0.5 0.5 | |||
0.5 0.0 0.5 | |||
2 | |||
cart | |||
0.00 0.00 0.00 | |||
0.25 0.25 0.25 | |||
=== {{FILE|INCAR}} === | |||
*This is the {{TAG|INCAR}} file for the basic DFT calculation: | |||
{{TAGBL|System}} = Si | |||
{{TAGBL|PREC}} = Normal ; {{TAGBL|ENCUT}} = 250.0 | |||
{{TAGBL|ISMEAR}} = 0 ; {{TAGBL|SIGMA}} = 0.01 | |||
{{TAGBL|KPAR}} = 2 | |||
{{TAGBL|EDIFF}} = 1.E-8 | |||
=== {{FILE|KPOINTS}} === | |||
Automatic | |||
0 | |||
Gamma | |||
6 6 6 | |||
0 0 0 | |||
== Calculation == | |||
*The workflow of GW0+BSE calculations is given in doall.sh and consists of the following consecutive steps: | |||
# "Standard" DFT groundstate calculation. | |||
# Obtain virtual orbitals: needs {{TAG|WAVECAR}} file from step 1. | |||
# The GW0 calculation: need {{TAG|WAVECAR}} and {{TAG|WAVEDER}} from step 2. | |||
# Optional step: use {{TAG|LOPTICS}}=''.TRUE.'' to plot dielectric function in the independent particle approximation (IPA) using GW0 quasiparticle energies instead of DFT energies. | |||
# The BSE calculation: needs {{TAG|WAVECAR}} from step 3 and {{TAG|WAVEDER}} from step 2. | |||
=== Step 1: DFT groundstate calculation === | |||
*We perform standard DFT calculation using the INCAR.DFT file. | |||
=== Step 2: Obtain DFT "virtual" orbitals (empty states) === | |||
*This step uses the INCAR.DIAG file: | |||
{{TAGBL|System}} = Si | |||
{{TAGBL|PREC}} = Normal ; {{TAGBL|ENCUT}} = 250.0 | |||
{{TAGBL|ALGO}} = EXACT ; {{TAGBL|NELM}} = 1 | |||
{{TAGBL|ISMEAR}} = 0 ; {{TAGBL|SIGMA}} = 0.01 | |||
{{TAGBL|KPAR}} = 2 | |||
{{TAGBL|NBANDS}} = 128 | |||
{{TAGBL|LOPTICS}} = .TRUE. ; {{TAGBL|LPEAD}} = .TRUE. | |||
{{TAGBL|OMEGAMAX}} = 40 | |||
*We use exact diagonalization for this step ({{TAG|ALGO}}=''EXACT'') and keep 128 bands after diagonalization ({{TAG|NBANDS}}=128). | |||
*With {{TAG|LPEAD}}=''.TRUE.'' we use an alternative way of computing the derivates of the orbitals with respect to the Bloch wave vectors. | |||
*It is important that this calculations needs the orbitals ({{TAG|WAVECAR}} file) written in step 1. | |||
=== Step 3: RPA quasiparticles with single-shot GW (G0W0) === | |||
*This step uses the INCAR.GW0 file: | |||
{{TAGBL|System}} = Si | |||
{{TAGBL|PREC}} = Normal ; {{TAGBL|ENCUT}} = 250.0 | |||
{{TAGBL|ALGO}} = GW0 | |||
{{TAGBL|ISMEAR}} = 0 ; {{TAGBL|SIGMA}} = 0.01 | |||
{{TAGBL|ENCUTGW}} = 150 ; {{TAGBL|NELM}} = 1 ; {{TAGBL|NOMEGA}} = 50 ; {{TAGBL|OMEGATL}} = 280 | |||
{{TAGBL|KPAR}} = 2 | |||
#{{TAGBL|NBANDSO}}=4 ; {{TAGBL|NBANDSV}}=8 ; {{TAGBL|LADDER}}=.TRUE. ; {{TAGBL|LUSEW}}=.TRUE. | |||
{{TAGBL|NBANDS}} = 128 | |||
{{TAGBL|NBANDSGW}} = 12 | |||
{{TAGBL|LWAVE}} = .TRUE. | |||
{{TAGBL|PRECFOCK}} = Normal | |||
*We select the G0W0 method by specifying {{TAG|ALGO}}=''GW0'' and {{TAG|NELM}}=1. | |||
*The energy cut off for the response function is select by {{TAG|ENCUTGW}}. | |||
*The number of point used in the frequency integration is given by {{TAG|NOMEGA}}. | |||
*Use the same number of bands ({{TAG|NBANDS}}) as in step 2, otherwise the {{TAG|WAVEDER}} file is not read correctly. | |||
*The quasiparticle energies are calculated for the first few bands given by {{TAG|NBANDSGW}}. | |||
*It is important that this calculation needs the orbitals ({{TAG|WAVECAR}} file) and the derivatives of the orbitals with respect to the Bloch vectors ({{TAG|WAVEDER}} file). | |||
*The quasiparticle energies can be found in the {{TAG|OUTCAR}} file (saved as OUTCAR.GW0 in this example): | |||
QP shifts <psi_nk| G(iteration)W_0 |psi_nk>: iteration 1 | |||
for sc-GW calculations column KS-energies equals QP-energies in previous step | |||
and V_xc(KS)= KS-energies - (<T + V_ion + V_H > + <T+V_H+V_ion>^1 + <V_x>^1) | |||
k-point 1 : 0.0000 0.0000 0.0000 | |||
band No. KS-energies QP-energies sigma(KS) V_xc(KS) V^pw_x(r,r') Z occupation | |||
=== Step 4 (optional): Plot IPA dielectric function using GW0 quasiparticle energies === | |||
* This step uses the INCAR.NONE file: | |||
{{TAGBL|System}} = Si | |||
{{TAGBL|PREC}} = Normal ; {{TAGBL|ENCUT}} = 250.0 | |||
{{TAGBL|ALGO}} = Nothing ; {{TAGBL|NELM}} = 1 | |||
{{TAGBL|ISMEAR}} = 0 ; {{TAGBL|SIGMA}} = 0.01 | |||
{{TAGBL|KPAR}} = 2 | |||
{{TAGBL|NBANDS}} = 128 | |||
{{TAGBL|LWAVE}} = .FALSE. | |||
{{TAGBL|LOPTICS}} = .TRUE. ; {{TAGBL|LPEAD}} = .TRUE. | |||
{{TAGBL|OMEGAMAX}} = 40 | |||
*By specyfing {{TAG|ALGO}}=''Nothing'' we do nothing except reading the {{TAG|WAVECAR}} file. | |||
*Using {{TAG|LOPTICS}}=''.TRUE.'' and {{TAG|LPEAD}}=''.TRUE.'' we compute the dielectric function in the IPA. | |||
=== Step 5: The BSE calculation === | |||
* This step uses the INCAR.BSE file: | |||
{{TAGBL|PREC}} = Normal ; {{TAGBL|ENCUT}} = 250.0 | |||
{{TAGBL|ALGO}} = BSE | |||
{{TAGBL|ANTIRES}} = 0 | |||
{{TAGBL|ISMEAR}} = 0 ; {{TAGBL|SIGMA}} = 0.01 | |||
{{TAGBL|ENCUTGW}} = 150 | |||
{{TAGBL|EDIFF}} = 1.E-8 | |||
{{TAGBL|NBANDS}} = 128 | |||
{{TAGBL|NBANDSO}} = 4 | |||
{{TAGBL|NBANDSV}} = 8 | |||
{{TAGBL|OMEGAMAX}} = 20 | |||
{{TAGBL|PRECFOCK}} = Normal | |||
*By specifying {{TAG|ANTIRES}}=0 we use the Tamm-Dancoff approximation. | |||
*{{TAG|ENCUTGW}}=150 specifies the energy cut-off of the response function. | |||
*{{TAG|NBANDSO}} and {{TAG|NBANDSV}} define the number of valence and conduction bands in the calculations. | |||
*This calculation needs the orbitals ({{TAG|WAVECAR}} file) from step 3 and the derivative of the orbitals with respect to the Bloch vectors ({{TAG|WAVEDER}} file) written in step 2. | |||
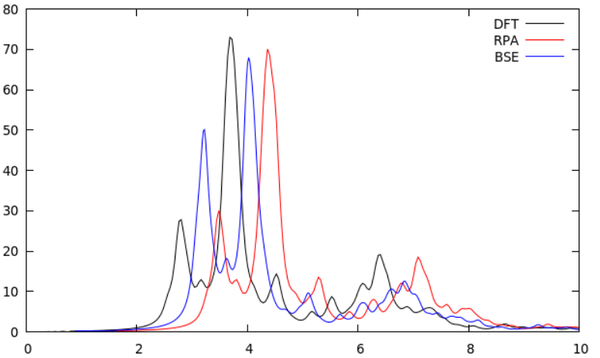
*By using the script ./plotall.sh we get the absorption spectra within the independent particle picture and with BSE: | |||
[[File:Fig BSE example1 2.png|600px]] | |||
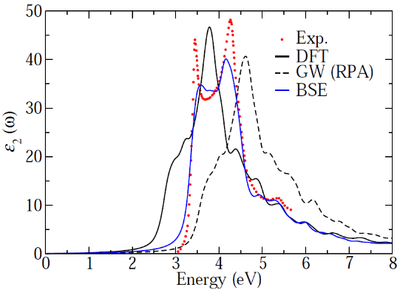
*The calculated dielectric function of Si is at this point (GW+BSE) already in much better agreement with experiment. However we can do even better as shown in the following figure: | |||
[[File:Fig BSE example1 4.png|400px]] | |||
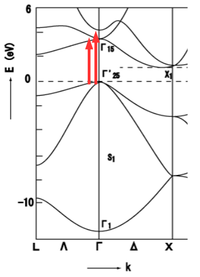
*The problem comes from the coarse k-point grid that we have used. A denser grid samples more (direct) transitions between the bands. | |||
[[File:Fig BSE example1 3.png|200px]] | |||
*Simply using a denser grid is mostly not an option because of the computational expense. | |||
---- | ---- | ||
== Download == | == Download == | ||
[ | [[Media:Si BSE.tgz| Si_BSE.tgz]] | ||
{{Template:BSE}} | |||
[[Category:Examples]] | [[Category:Examples]] | ||
Latest revision as of 13:20, 14 November 2019
Overview > Dielectric properties of Si using BSE > Improving the dielectric function > Plotting the BSE fatband structure of Si > List of tutorials
Task
Description: Calculate the dielectric function of Si including excitonic effects by solving the Bethe-Salpeter equation (BSE) on top of GW0.
Input
POSCAR
Si 5.4300 0.5 0.5 0.0 0.0 0.5 0.5 0.5 0.0 0.5 2 cart 0.00 0.00 0.00 0.25 0.25 0.25
INCAR
- This is the INCAR file for the basic DFT calculation:
System = Si PREC = Normal ; ENCUT = 250.0 ISMEAR = 0 ; SIGMA = 0.01 KPAR = 2 EDIFF = 1.E-8
KPOINTS
Automatic 0 Gamma 6 6 6 0 0 0
Calculation
- The workflow of GW0+BSE calculations is given in doall.sh and consists of the following consecutive steps:
- "Standard" DFT groundstate calculation.
- Obtain virtual orbitals: needs WAVECAR file from step 1.
- The GW0 calculation: need WAVECAR and WAVEDER from step 2.
- Optional step: use LOPTICS=.TRUE. to plot dielectric function in the independent particle approximation (IPA) using GW0 quasiparticle energies instead of DFT energies.
- The BSE calculation: needs WAVECAR from step 3 and WAVEDER from step 2.
Step 1: DFT groundstate calculation
- We perform standard DFT calculation using the INCAR.DFT file.
Step 2: Obtain DFT "virtual" orbitals (empty states)
- This step uses the INCAR.DIAG file:
System = Si PREC = Normal ; ENCUT = 250.0 ALGO = EXACT ; NELM = 1 ISMEAR = 0 ; SIGMA = 0.01 KPAR = 2 NBANDS = 128 LOPTICS = .TRUE. ; LPEAD = .TRUE. OMEGAMAX = 40
- We use exact diagonalization for this step (ALGO=EXACT) and keep 128 bands after diagonalization (NBANDS=128).
- With LPEAD=.TRUE. we use an alternative way of computing the derivates of the orbitals with respect to the Bloch wave vectors.
- It is important that this calculations needs the orbitals (WAVECAR file) written in step 1.
Step 3: RPA quasiparticles with single-shot GW (G0W0)
- This step uses the INCAR.GW0 file:
System = Si PREC = Normal ; ENCUT = 250.0 ALGO = GW0 ISMEAR = 0 ; SIGMA = 0.01 ENCUTGW = 150 ; NELM = 1 ; NOMEGA = 50 ; OMEGATL = 280 KPAR = 2 #NBANDSO=4 ; NBANDSV=8 ; LADDER=.TRUE. ; LUSEW=.TRUE. NBANDS = 128 NBANDSGW = 12 LWAVE = .TRUE. PRECFOCK = Normal
- We select the G0W0 method by specifying ALGO=GW0 and NELM=1.
- The energy cut off for the response function is select by ENCUTGW.
- The number of point used in the frequency integration is given by NOMEGA.
- Use the same number of bands (NBANDS) as in step 2, otherwise the WAVEDER file is not read correctly.
- The quasiparticle energies are calculated for the first few bands given by NBANDSGW.
- It is important that this calculation needs the orbitals (WAVECAR file) and the derivatives of the orbitals with respect to the Bloch vectors (WAVEDER file).
- The quasiparticle energies can be found in the OUTCAR file (saved as OUTCAR.GW0 in this example):
QP shifts <psi_nk| G(iteration)W_0 |psi_nk>: iteration 1 for sc-GW calculations column KS-energies equals QP-energies in previous step and V_xc(KS)= KS-energies - (<T + V_ion + V_H > + <T+V_H+V_ion>^1 + <V_x>^1) k-point 1 : 0.0000 0.0000 0.0000 band No. KS-energies QP-energies sigma(KS) V_xc(KS) V^pw_x(r,r') Z occupation
Step 4 (optional): Plot IPA dielectric function using GW0 quasiparticle energies
- This step uses the INCAR.NONE file:
System = Si PREC = Normal ; ENCUT = 250.0 ALGO = Nothing ; NELM = 1 ISMEAR = 0 ; SIGMA = 0.01 KPAR = 2 NBANDS = 128 LWAVE = .FALSE. LOPTICS = .TRUE. ; LPEAD = .TRUE. OMEGAMAX = 40
- By specyfing ALGO=Nothing we do nothing except reading the WAVECAR file.
- Using LOPTICS=.TRUE. and LPEAD=.TRUE. we compute the dielectric function in the IPA.
Step 5: The BSE calculation
- This step uses the INCAR.BSE file:
PREC = Normal ; ENCUT = 250.0 ALGO = BSE ANTIRES = 0 ISMEAR = 0 ; SIGMA = 0.01 ENCUTGW = 150 EDIFF = 1.E-8 NBANDS = 128 NBANDSO = 4 NBANDSV = 8 OMEGAMAX = 20 PRECFOCK = Normal
- By specifying ANTIRES=0 we use the Tamm-Dancoff approximation.
- ENCUTGW=150 specifies the energy cut-off of the response function.
- NBANDSO and NBANDSV define the number of valence and conduction bands in the calculations.
- This calculation needs the orbitals (WAVECAR file) from step 3 and the derivative of the orbitals with respect to the Bloch vectors (WAVEDER file) written in step 2.
- By using the script ./plotall.sh we get the absorption spectra within the independent particle picture and with BSE:
- The calculated dielectric function of Si is at this point (GW+BSE) already in much better agreement with experiment. However we can do even better as shown in the following figure:
- The problem comes from the coarse k-point grid that we have used. A denser grid samples more (direct) transitions between the bands.
- Simply using a denser grid is mostly not an option because of the computational expense.